题目内容
设函数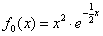 ,记
,记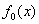 的导函数
的导函数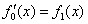 ,
,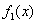 的导函数
的导函数
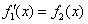 ,
,
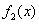 的导函数
的导函数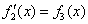 ,…,
,…,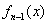 的导函数
的导函数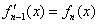 ,
,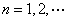 .
.
(1)求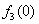 ;
;
(2)用n表示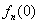 ;
;
(3)设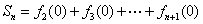 ,是否存在
,是否存在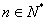 使
使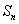 最大?证明你的结论.
最大?证明你的结论.
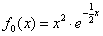 ,记
,记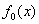 的导函数
的导函数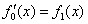 ,
,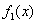 的导函数
的导函数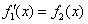 ,
,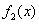 的导函数
的导函数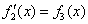 ,…,
,…,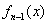 的导函数
的导函数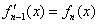 ,
,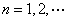 .
.(1)求
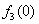 ;
;(2)用n表示
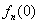 ;
;(3)设
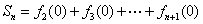 ,是否存在
,是否存在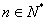 使
使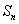 最大?证明你的结论.
最大?证明你的结论.(1)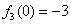 (2)
(2)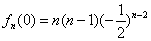 (3)故当
(3)故当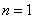 或
或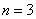 时,
时,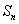 取
取
最大值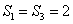 .
.
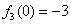 (2)
(2)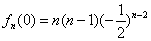 (3)故当
(3)故当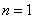 或
或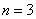 时,
时,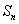 取
取最大值
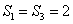 .
.试题分析:⑴易得,
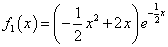 ,
, 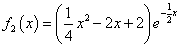
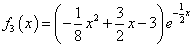 ,所以
,所以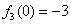
⑵不失一般性,设函数
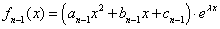 的导函数为
的导函数为 ,其中
,其中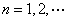 ,常数
,常数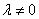 ,
,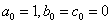 .
.对
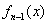 求导得:
求导得: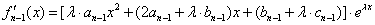
故由
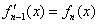 得:
得: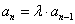 ①,
①,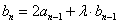 ②,
②, 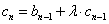 ③
③ 由①得:
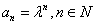 ,
, 代入②得:
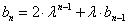 ,即
,即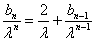 ,其中
,其中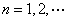
故得:
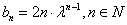 .
. 代入③得:
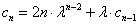 ,即
,即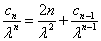 ,其中
,其中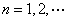 .
. 故得:
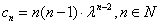 ,
, 因此
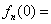
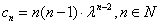 .
.将
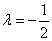 代入得:
代入得: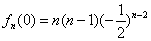 ,其中
,其中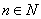 .
. (3)由(1)知
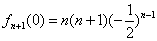 ,
,当
 时,
时,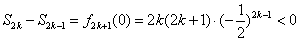 ,
,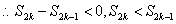 ,故当
,故当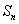 最大时,
最大时,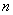 为奇数.
为奇数. 当
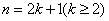 时,
时,
又
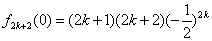 ,
,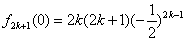
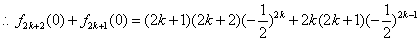
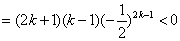 ,
,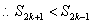 ,因此数列
,因此数列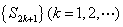 是递减数列
是递减数列 又
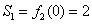 ,
,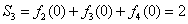 ,
, 故当
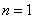 或
或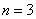 时,
时,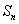 取最大值
取最大值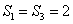 .
. 点评:本题是数列综合题,利用转化法把非常规数列转化成等差或等比数列来处理是关键,
属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
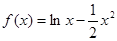 在[
在[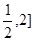 上的极大值是 .
上的极大值是 .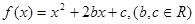
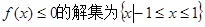 ,求实数b,c的值;
,求实数b,c的值;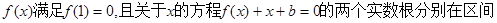
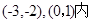 求实数
求实数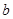 的取值范围.
的取值范围.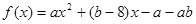 ,当
,当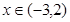 时,
时,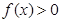 ;
;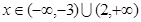 时,
时,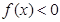
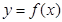 的解析式
的解析式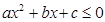 的解集为R.
的解集为R.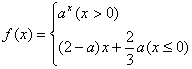 在
在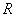 上为增函数,则
上为增函数,则 的取值范围是 (用区间表示)
的取值范围是 (用区间表示)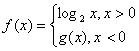 是偶函数,则
是偶函数,则 的值等于( )
的值等于( )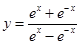 的图象大致为( ).
的图象大致为( ).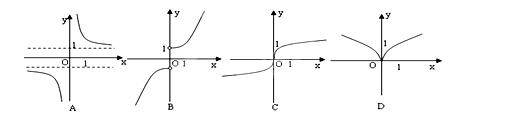
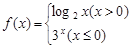 ,则
,则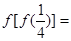 .
. 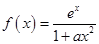 ,其中
,其中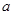 为正实数.
为正实数.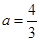 时,求
时,求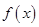 的极值点;
的极值点;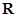 上的单调函数,求
上的单调函数,求