题目内容
设点O为坐标原点,直线l: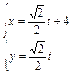 (参数t∈R)与曲线C:
(参数t∈R)与曲线C: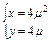 (参数
(参数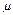 ∈R)交于A,B两点.
∈R)交于A,B两点.
(1)求直线l与曲线C的直角坐标方程;
(2)求证:OA⊥OB.
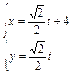 (参数t∈R)与曲线C:
(参数t∈R)与曲线C: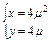 (参数
(参数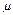 ∈R)交于A,B两点.
∈R)交于A,B两点.(1)求直线l与曲线C的直角坐标方程;
(2)求证:OA⊥OB.
(1)直线l的普通方程为:x-y-4=0.曲线C的普通方程为:y2=4x.
(2)证明略
(2)证明略
(1) 直线l的普通方程为:x-y-4=0.曲线C的普通方程为:y2=4x.
(2)证明 设A(x1,y1),B(x2,y2),由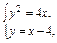
消去y,得x2-12x+16=0,∴x1+x2=12,x1x2=16,
∴kOA·kOB=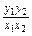 =
=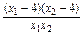
=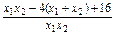 =-1,∴OA⊥OB.
=-1,∴OA⊥OB.
(2)证明 设A(x1,y1),B(x2,y2),由
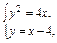
消去y,得x2-12x+16=0,∴x1+x2=12,x1x2=16,
∴kOA·kOB=
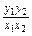 =
=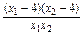
=
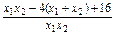 =-1,∴OA⊥OB.
=-1,∴OA⊥OB.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
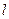 的参数方程为
的参数方程为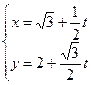 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为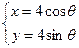 (θ为参数).
(θ为参数).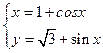 (q为参数)表示的曲线为C,求在曲线C上到原点O距离最小的点P的坐标.
(q为参数)表示的曲线为C,求在曲线C上到原点O距离最小的点P的坐标. 的直线l和椭圆
的直线l和椭圆 =1交于A,B两点,求线段AB的长度及点M(-1,1)到A,B两点的距离之积.
=1交于A,B两点,求线段AB的长度及点M(-1,1)到A,B两点的距离之积.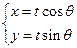 与圆
与圆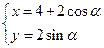 相切,则
相切,则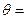 _______________。
_______________。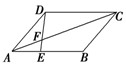
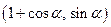 ,参数
,参数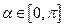 ,点Q在直线
,点Q在直线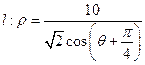 上,求
上,求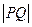 的最大值。
的最大值。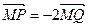 ,则点M的轨迹方程是 .
,则点M的轨迹方程是 . 
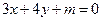 与圆
与圆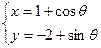 (
(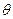 为参数)相切,则实数m的值是_______
为参数)相切,则实数m的值是_______