题目内容
已知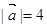 ,
,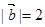 ,且
,且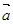 与
与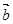 夹角为120°求
夹角为120°求
(1)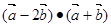 ; (2)
; (2)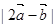 ; (3)
; (3)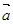 与
与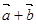 的夹角
的夹角
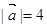 ,
,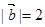 ,且
,且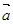 与
与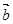 夹角为120°求
夹角为120°求(1)
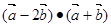 ; (2)
; (2)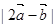 ; (3)
; (3)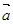 与
与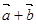 的夹角
的夹角
试题分析:(1)根据题意,由于
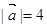 ,
,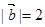 ,且
,且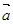 与
与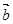 夹角为120°,那么可知
夹角为120°,那么可知
(2)
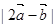 =
=

(3)根据题意,由于
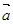 与
与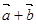 的夹角公式为,cos<
的夹角公式为,cos<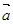 ,
,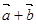 >=
>=
 ,故可知
,故可知 。
。点评:主要是考查两个向量的数量积公式的应用,求向量的模,属于中档题.

练习册系列答案
相关题目
题目内容
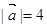 ,
,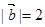 ,且
,且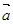 与
与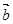 夹角为120°求
夹角为120°求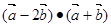 ; (2)
; (2)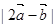 ; (3)
; (3)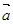 与
与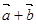 的夹角
的夹角
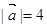 ,
,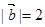 ,且
,且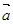 与
与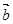 夹角为120°,那么可知
夹角为120°,那么可知
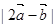 =
=

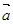 与
与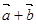 的夹角公式为,cos<
的夹角公式为,cos<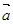 ,
,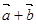 >=
>=
 ,故可知
,故可知 。
。