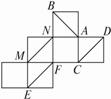
题目内容
如图(1),△BCD内接于直角梯形A1A2A3D,已知沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图(2)所示.

(1)求证:在三棱锥ABCD中,AB⊥CD;
(2)若直角梯形的上底A1D=10,高A1A2=8,求翻折后三棱锥的侧面ACD与底面BCD所成二面角θ的余弦值.

(1)求证:在三棱锥ABCD中,AB⊥CD;
(2)若直角梯形的上底A1D=10,高A1A2=8,求翻折后三棱锥的侧面ACD与底面BCD所成二面角θ的余弦值.
(1)证明:在直角梯形A1A2A3D中,
A1D⊥A1B,A2C⊥A2B,
翻折成三棱锥后仍有AB⊥AD,AB⊥AC,
∴AB⊥平面ACD.
又
 平面ACD,∴AB⊥CD.
平面ACD,∴AB⊥CD.(2)解:由题设可知,B、C必是A1A2、A2A3的中点,A1D=A3D.
∴A1D=A3D=10,A1B=A2B=4.

过D作DE⊥A2A3,垂足为E,得DE=8.
在Rt△DEA3中,得EA3=6,
∴A2A3=16.
于是A2C=CA3=8,CE=2.
不难得到S△BCD=36,S△CDA=32.
∵AB⊥平面ACD,
由面积射影定理得
 .
.故侧面ACD与底面BCD所成二面角θ的余弦值为
 .
.空间直线和平面

练习册系列答案
相关题目
 中,
中,  底面
底面 ,
,
 .
.
 分别为棱
分别为棱 的中点,求证:
的中点,求证: 平面
平面 ;
; 中,底面是一个矩形,
中,底面是一个矩形, ,
, ,又
,又 ,
, ,
, .
. 的大小.(用反三角函数表示)
的大小.(用反三角函数表示)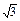 ,EF=2.
,EF=2.
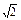 ,求点A到平面PEC的距离.
,求点A到平面PEC的距离.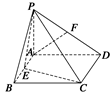
 平面
平面 ,
, ,
, 是夹在两平行平面间的两条线段,
是夹在两平行平面间的两条线段, ,
, 在
在 内,
内, ,
, 在
在 ,
, 分别在
分别在 .求证:
.求证: .
.