题目内容
若无穷等比数列{an}的前n项和为Sn，首项为1，公比为a-
，且
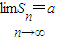，（n∈N*），则复数z=
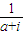在复平面上对应的点位于（ ）A．第一象限
B．第二象限
C．第三象限
D．第四象限
【答案】分析：利用无穷等比数列的求和公式，求出a的值，再化简复数，即可求得结论．
解答：解：∵无穷等比数列{an}的前n项和为Sn，首项为1，公比为a-
，且
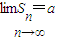，（n∈N*），
∴
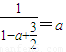
∴2a2-5a+2=0
∴a=2或a=
∴a-
=
或a-
=-1
∵|a-
|＜1
∴a=2
∴z=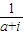
=
=
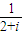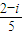
∴复数z=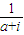
在复平面上对应的点位于第四象限
故选D．
点评：本题考查无穷等比数列的求和公式，考查数列的极限，考查复数的几何意义，属于中档题．
解答：解：∵无穷等比数列{an}的前n项和为Sn，首项为1，公比为a-
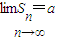，且，（n∈N*），∴
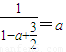
∴2a2-5a+2=0
∴a=2或a=
∴a-
=或a-=-1∵|a-
|＜1∴a=2
∴z=
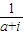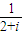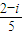
==∴复数z=
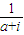在复平面上对应的点位于第四象限故选D．
点评：本题考查无穷等比数列的求和公式，考查数列的极限，考查复数的几何意义，属于中档题．
练习册系列答案
相关题目