题目内容
(本题满分12分)
已知函数 ,
,  .
.
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2)设函数 在
在 上的图象与
上的图象与 轴的交点从左到右分别为M、N,图象的最高点为P,
轴的交点从左到右分别为M、N,图象的最高点为P,
求 与
与 的夹角的余弦.
的夹角的余弦.
已知函数
 ,
,  .
.(1)求函数
 的最大值和最小值;
的最大值和最小值;(2)设函数
 在
在 上的图象与
上的图象与 轴的交点从左到右分别为M、N,图象的最高点为P,
轴的交点从左到右分别为M、N,图象的最高点为P, 求
 与
与 的夹角的余弦.
的夹角的余弦.(1)2,-2.-
(2)

 .
.解:(1)∵ =
=
= ------------------------------------4分
------------------------------------4分
∵ ∴
∴ ,
,
∴函数 的最大值和最小值分别为2,-2.---------------6分
的最大值和最小值分别为2,-2.---------------6分
(2)解法1:令 得
得 ,
,
∵ ∴
∴ 或
或
∴ -----------------------8分
-----------------------8分
由 ,且
,且 得
得 ∴
∴ -------------------9分
-------------------9分
∴ 从而
从而
∴
 .------------------------------12分
.------------------------------12分
解法2:过点P作 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,---8分
,---8分
 ,--------------------------------9分
,--------------------------------9分
由余弦定理得 =
= .---12分
.---12分
解法3:过点P作 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,---8分
,---8分
 -------------------------------9分
-------------------------------9分
在 中,
中, ------------11分
------------11分
∵PA平分 ∴
∴
 .------------------------------12分
.------------------------------12分
 =
=
=
 ------------------------------------4分
------------------------------------4分∵
 ∴
∴ ,
,∴函数
 的最大值和最小值分别为2,-2.---------------6分
的最大值和最小值分别为2,-2.---------------6分(2)解法1:令
 得
得 ,
,∵
 ∴
∴ 或
或
∴
 -----------------------8分
-----------------------8分由
 ,且
,且 得
得 ∴
∴ -------------------9分
-------------------9分∴
 从而
从而∴

 .------------------------------12分
.------------------------------12分解法2:过点P作
 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,---8分
,---8分 ,--------------------------------9分
,--------------------------------9分由余弦定理得
 =
= .---12分
.---12分解法3:过点P作
 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,---8分
,---8分 -------------------------------9分
-------------------------------9分在
 中,
中, ------------11分
------------11分∵PA平分
 ∴
∴
 .------------------------------12分
.------------------------------12分
练习册系列答案
相关题目
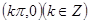 是正弦曲线的对称中心;(2)点
是正弦曲线的对称中心;(2)点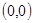 是余弦曲线的一个对称中心;(3)把余弦函数
是余弦曲线的一个对称中心;(3)把余弦函数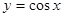 的图像向左平移
的图像向左平移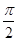 个单位,即得
个单位,即得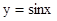 的图像;(4)在余弦曲线
的图像;(4)在余弦曲线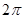 ;(5)在正弦曲线
;(5)在正弦曲线 中,相邻两个最高点的水平距离是
中,相邻两个最高点的水平距离是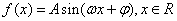 (其中
(其中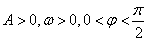 )的最小正周期为
)的最小正周期为 ,且图象上一个最高点为
,且图象上一个最高点为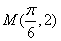 。
。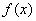 的解析式;
的解析式;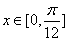 ,求:
,求: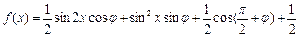 ,
,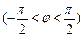 ,其图象过点
,其图象过点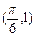
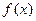 的解析式,并求对称中心
的解析式,并求对称中心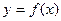 的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到
的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到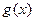 的图象,求函数
的图象,求函数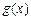 在
在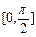 上的最大值和最小值.
上的最大值和最小值.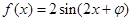 的图像如图所示,
的图像如图所示, ,则
,则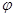 的值为 ( )
的值为 ( )

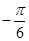


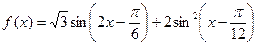 (
(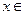 R).
R).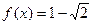 且
且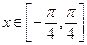 ,求x;(Ⅱ)求函数
,求x;(Ⅱ)求函数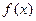 的单调递增区间.
的单调递增区间.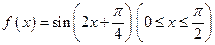 的单调递增区间是 ▲ .
的单调递增区间是 ▲ .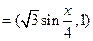 ,n
,n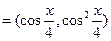 ,函数
,函数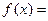 m·n.
m·n.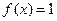 ,求
,求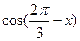 的值;
的值;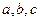 ,且满足
,且满足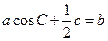 ,求
,求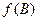 的取值范围.
的取值范围.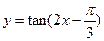 的周期为 ▲ .
的周期为 ▲ .