题目内容
6.已知函数f(x)=x2+ax-lnx(a∈R).(Ⅰ)当a=0时,求f(x)的单调区间与极值;
(Ⅱ)令g(x)=f(x)-x2,若函数g(x)在x∈(0,e]的最小值为3,求实数a的值.
分析 (Ⅰ)根据导数和函数的单调性以及极值的关系即可求出
(Ⅱ)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值
解答 解:(Ⅰ)当a=0时,f(x)=x2-lnx(a∈R)的定义域为(0,+∞).$f(x)=2x-\frac{1}{x}=\frac{{2{x^2}-1}}{x}=\frac{{(\sqrt{2}x-1)(\sqrt{2}x+1)}}{x}(x>0)$,画图列表如下:
| x | $(0,\frac{1}{{\sqrt{2}}})$ | $(\frac{1}{{\sqrt{2}}},+∞)$ | |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
∴f(x)的极小值为$f(\frac{1}{{\sqrt{2}}})=\frac{1}{2}+\frac{1}{2}ln2$,无极大值;
(Ⅱ)g(x)=f(x)-x2=ax-lnx的定义域为(0,e],
$g'(x)=a-\frac{1}{x}=\frac{ax-1}{x}(0<x≤e)$的正负号等价于h(x)=ax-1(0<x≤e)的正负号.
当a≠0时,g'(x)=0与h(x)=0的根相同为${x_0}=\frac{1}{a}$,
①当a<0时,${x_0}=\frac{1}{a}<0$,h(x)<0⇒g'(x)<0⇒g(x)在(0,e]上递减,
∴$g{(x)_{min}}=g(e)=ae-1=3⇒a=\frac{4}{e}$⇒a∈∅;
②当a=0时,$g'(x)=-\frac{1}{x}<0$⇒g(x)在(0,e]上递减,
∴$g{(x)_{min}}=g(e)=ae-1=3⇒a=\frac{4}{e}$⇒a∈∅;
③当$0<a≤\frac{1}{e}$时,$e<{x_0}=\frac{1}{a}$,h(x)≤0⇒g'(x)≤0⇒g(x)在(0,e]上递减,
∴$g{(x)_{min}}=g(e)=ae-1=3⇒a=\frac{4}{e}$⇒a∈∅;
④当$\frac{1}{e}$<a时,$0<{x_0}=\frac{1}{a}<e$,列表如下:
| x | (0,x0) | x0 | (x0,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
综上可得:a=e2.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程,考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,是中档题

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
1.已知i为虚数单位,则$|{\frac{2-i}{1+i}}|$=( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{{\sqrt{17}}}{2}$ | D. | $\frac{{\sqrt{10}}}{2}$ |
2.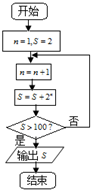 执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )
执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )
 执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )
执行如图所示的程序框图,若将判断框内“S>100”改为关于n的不等式“n≥n0”且要求输出的结果不变,则正整数n0的取值( )| A. | 是4 | B. | 是5 | C. | 是6 | D. | 不唯一 |
16.已知函数f(x)=2sin(ωx)(其中常数ω>0),若存在x1∈[-$\frac{2π}{3}$,0],x2∈(0,$\frac{π}{4}$],使f(x1)=f(x2),则ω的取值范围为( )
| A. | ($\frac{3}{2}$,4) | B. | ($\frac{3}{2}$,+∞) | C. | (4,+∞) | D. | (0,$\frac{3}{2}$) |
 在四棱锥P-ABCD中,底面四边形ABCD中,AB=AD=2$\sqrt{3}$,CD=BC=2,PA=2,AB⊥BC,PA⊥CD,面PAB⊥面ABCD.
在四棱锥P-ABCD中,底面四边形ABCD中,AB=AD=2$\sqrt{3}$,CD=BC=2,PA=2,AB⊥BC,PA⊥CD,面PAB⊥面ABCD.