题目内容
已知等比数列{an}的各项均为正数,数列{bn}满足bn=lgan,b3=18,b6=12,数列{bn}的前n项和为Sn,则使得Sn达到最大值的n是( )A.11
B.12
C.10或11
D.11或12
【答案】分析:根据bn=lgan,推断出an=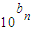 ,进而表示出a3和a6,联立方程求得公比q,进而根据等比数列的通项公式求得an,进而求得bn,然后令bn≥0求得n的范围,答案可得.
,进而表示出a3和a6,联立方程求得公比q,进而根据等比数列的通项公式求得an,进而求得bn,然后令bn≥0求得n的范围,答案可得.
解答:解:bn=lgan⇒an=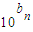 ,
,
∴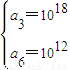 ,
,
∴ ,
,
∴q=10-2∴an=a3qn-3=1024-2n
∴bn=24-2n令bn≥0⇒n≤12,
∴当n=11或12时,Sn最大,
故选D.
点评:本题主要考查了等比数列的性质和等比数列的通项公式.考查了学生对基础知识的综合运用.
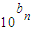 ,进而表示出a3和a6,联立方程求得公比q,进而根据等比数列的通项公式求得an,进而求得bn,然后令bn≥0求得n的范围,答案可得.
,进而表示出a3和a6,联立方程求得公比q,进而根据等比数列的通项公式求得an,进而求得bn,然后令bn≥0求得n的范围,答案可得.解答:解:bn=lgan⇒an=
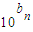 ,
,∴
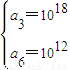 ,
,∴
 ,
,∴q=10-2∴an=a3qn-3=1024-2n
∴bn=24-2n令bn≥0⇒n≤12,
∴当n=11或12时,Sn最大,
故选D.
点评:本题主要考查了等比数列的性质和等比数列的通项公式.考查了学生对基础知识的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目