题目内容
11. 一个多边形的直观图和三视图如图所示(其中EMF分别是PB,AD的中心)
一个多边形的直观图和三视图如图所示(其中EMF分别是PB,AD的中心)(1)求证:EF⊥平面PBC;
(2)求三棱锥B-AEF的体积.
分析 (1)由三视图可知,四棱锥P-ABCD的底面为正方形,边长为a,侧棱PD⊥底面ABCD,PD=a,取PC中点G,连接EG、GD,可证四边形FEGD为矩形,得到EG⊥DG,再由已知得到DG⊥PC,由线面垂直的判断得到DG⊥平面PBC,进一步证得答案;
(2)把三棱锥B-AEF的体积转化为E-ABF的体积得答案.
解答 (1)证明:如图, 取PC的中点G,连结EG,GD,则
取PC的中点G,连结EG,GD,则
EG∥BC,EG∥DF,EG=$\frac{1}{2}BC$,EG=$\frac{1}{2}DF$,
由三视图知FD⊥平面PDC,DG?面PDC,∴FD⊥DG,
∴四边形FEGD为矩形,
∵G为等腰Rt△PDC斜边PC的中点,
∴DG⊥PC,
又DG⊥GE,PC∩EG=G,
∴DG⊥平面PBC.
∵DG∥EF,∴EF⊥平面PBC;
(2)解:由三视图可知,四棱锥P-ABCD的底面为正方形,边长为a,侧棱PD⊥底面ABCD,PD=a,
又F为AD的中点,∴${S}_{△ABF}=\frac{1}{4}{a}^{2}$,
E为PB中点,则OE=$\frac{1}{2}PD=\frac{1}{2}a$,
∴VB-AEF=VE-ABF=$\frac{1}{3}$S△ABF•OE=$\frac{1}{3}•\frac{1}{4}{a}^{2}•\frac{1}{2}a=\frac{1}{24}{a}^{3}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.设命题甲为:sinαsinβ+cosαcosβ=0,命题乙为:sinαcosα+sinβcosβ=0,则甲是乙的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
16.在△ABC中,∠A=60°S△ABC=5$\sqrt{3}$,b=5,则sinBsinC的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{\sqrt{2}}{2}$ |
7.海中一小岛,周围anmile内有暗礁. 海轮由西向东航行,望见这岛在北偏东75°.航行bnmile以后,望见这岛在北偏东60°.这艘海轮不改变航向继续前进,没有触礁.那么a、b所满足的不等关系是( )
| A. | a<$\frac{1}{2}$b | B. | a>$\frac{1}{2}$b | C. | a<$\frac{\sqrt{3}}{2}$b | D. | a>$\frac{\sqrt{3}}{2}$b |
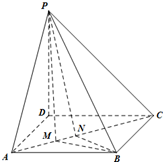 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,PD=AD=2,M,N分别为线段AC上的点.若∠MBN=30°,则三棱锥M-PNB体积的最小值为$\frac{4}{3}(2-\sqrt{3})$.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,PD=AD=2,M,N分别为线段AC上的点.若∠MBN=30°,则三棱锥M-PNB体积的最小值为$\frac{4}{3}(2-\sqrt{3})$.