题目内容
【题目】设函数![]() ,
,![]() ,其中
,其中![]() 、
、![]() .若
.若![]() 恒成立,则当
恒成立,则当![]() 取得最小值时,
取得最小值时,![]() 的值为______.
的值为______.
【答案】![]()
【解析】
构造函数![]() ,可知该函数关于点
,可知该函数关于点![]() 对称,然后分
对称,然后分![]() 、
、![]() 、
、![]() 三种情况讨论,分析函数
三种情况讨论,分析函数![]() 在区间
在区间![]() 上的单调性,得出函数
上的单调性,得出函数![]() 在区间
在区间![]() 上最值的可能取值,利用绝对值三角不等式可求出当
上最值的可能取值,利用绝对值三角不等式可求出当![]() 取得最小值时
取得最小值时![]() 的值.
的值.
构造函数![]() ,则
,则![]() ,
,
由于![]() ,
,
所以,函数![]() 的图象关于点
的图象关于点![]() 对称,且
对称,且![]() .
.
①当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则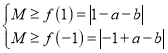 ,
,
所以![]() ,
,
此时,当![]() ,
,![]() 时,
时,![]() 取最小值
取最小值![]() ;
;
②当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则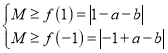 ,
,
所以![]() ,
,
此时,当![]() ,
,![]() 时,
时,![]() 取最小值
取最小值![]() ;
;
③当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
不妨设![]() ,则
,则![]() ,则
,则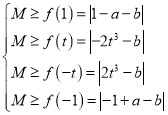 ,
,
![]() ,
,
![]() ,且
,且![]() ,
,![]() ,
,
![]() ,若
,若![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,但
,但![]() ,
,
![]() ,
,
所以,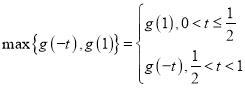 .
.
当![]() 时,
时,![]() ,
,
当且仅当![]() ,
,![]() 时,即当
时,即当![]() ,
,![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() .
.
综上所述,当![]() ,
,![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时
,此时![]() .
.
故答案为:![]() .
.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠(本次即第一次),标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 12 | 4 | 4 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人发放纪念品,求抽到的2人中恰有1人体检3次的概率.