题目内容
（2013•海口二模）选修4-1：几何证明选讲切线AB与圆切于点B，圆内有一点C满足AB=AC，∠CAB的平分线AE交圆于D，E，延长EC交圆于F，延长DC交圆于G，连接FG．
（Ⅰ）证明：AC∥FG；
（Ⅱ）求证：EC=EG．
分析：（Ⅰ）通过证明△ACD∽△AEC，推出∠ACD=∠AEC，然后证明AC∥FG
（Ⅱ）证明：连接BD，BE，EG，证明△ABD≌△ACD，△ABE≌△△ACE，然后证明BE=EG，
（Ⅱ）证明：连接BD，BE，EG，证明△ABD≌△ACD，△ABE≌△△ACE，然后证明BE=EG，
解答：证明：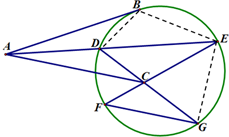
（Ⅰ）证明：∵AB切圆于B，
∴AB2=AD•AE，
又∵AB=AC，
∴AC2=AD•AE，
∴△ACD∽△AEC，
∴∠ACD=∠AEC，
又∵∠AEC=∠DGF，
∴∠ACD=∠DGF，∴AC∥FG （5分）
（Ⅱ）证明：连接BD，BE，EG
由AB=AC，∠BAD=∠DAC及AD=AD，知△ABD≌△ACD，同理有△ABE≌△ACE，
∴∠BDE=∠CDE，BE=CE
∴BE=EG，
∴EC=EG （10分）
（Ⅰ）证明：∵AB切圆于B，∴AB2=AD•AE，
又∵AB=AC，
∴AC2=AD•AE，
∴△ACD∽△AEC，
∴∠ACD=∠AEC，
又∵∠AEC=∠DGF，
∴∠ACD=∠DGF，∴AC∥FG （5分）
（Ⅱ）证明：连接BD，BE，EG
由AB=AC，∠BAD=∠DAC及AD=AD，知△ABD≌△ACD，同理有△ABE≌△ACE，
∴∠BDE=∠CDE，BE=CE
∴BE=EG，
∴EC=EG （10分）
点评：本题考查直线与圆的位置关系，三角形的全等与三角形相似定理的应用，考查逻辑推理能力．
练习册系列答案
相关题目
（2013•海口二模）已知集合M={-1，0，1}，N={0，1，2}，则如图所示韦恩图中的阴影部分所表示的集合为（ ）
（2013•海口二模）设偶函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π）的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL=1，则