题目内容
11.已知函数f(x)=$\frac{{e}^{x}}{{x}^{2}-ax+1}$(其中e为自然对数的底数,e=2.71828…).(1)当a=0时,求函数y=f(x)的图象在点x=0处的切线方程;
(2)当a∈(0,2)时,试求函数f(x)的极值;
(3)若a∈[0,$\frac{1}{2}$],则当x∈[0,a+1]时,函数y=f(x)的图象是否总在不等式y>x所表示的平面区域内,请写出判断过程.
分析 (1)a=0时求出f(x),f′(x),从而求得f(0),f′(0),也就是求出了切点和切线的斜率,从而根据点斜式方程写出切线方程即可;
(2)求出f′(x),根据a的范围,判断导数符号,根据极值的概念便可得出f(x)的极值;
(3)根据(2)便可写出f(x)在[0,a+1]上的单调性,可画出f(x)及y=x的大致图象,根据图象可以看出要使f(x)的图象在y>x表示的区域,只需f(a+1)>a+1,即f(a+1)-a-1>0恒成立.可设g(a)=$\frac{{e}^{a+1}}{a+2}-a-1$,通过求g′(a),g″(a),便可判断g(a)在[0,$\frac{1}{2}$]上单调递增,从而得出g(a)>0成立,从而得出函数y=f(x)的图象总在不等式y>x所表示的平面区域内.
解答 解:(1)a=0时,f(x)=$\frac{{e}^{x}}{{x}^{2}+1}$,$f′(x)=\frac{{e}^{x}(x-1)^{2}}{({x}^{2}+1)^{2}}$;
∴f′(0)=1,又f(0)=1;
∴所求切线方程的斜率为1,切点为(0,1);
∴f(x)在x=0处切线方程为y-1=x,即y=x+1;
(2)$f′(x)=\frac{{e}^{x}[{x}^{2}-(a+2)x+a+1]}{({x}^{2}-ax+1)^{2}}$=$\frac{{e}^{x}(x-1)[x-(a+1)]}{({x}^{2}-ax+1)^{2}}$;
∵a∈(0,2),∴x2-ax+1>0恒成立,且1<a+1;
∴x∈(-∞,1)时,f′(x)>0,x∈(1,a+1)时,f′(x)<0,x∈(a+1,+∞)时,f′(x)>0;
∴x=1时,f(x)取得极大值$\frac{e}{2-a}$,x=a+1时,f(x)取得极小值$\frac{{e}^{a+1}}{a+2}$;
(3)由(2)知,x∈[0,1)时,f′(x)>0;x∈(1,a+1),f′(x)<0;
∴f(x)在[0,1]上单调递增,在(1,a+1]上单调递减,f(1)=$\frac{e}{2-a}$是f(x)在[0,a+1]上的最大值;
假设函数y=f(x)的图象总在不等式y>x所表示的平面区域内,则f(x)及y=x的大致图象如下所示: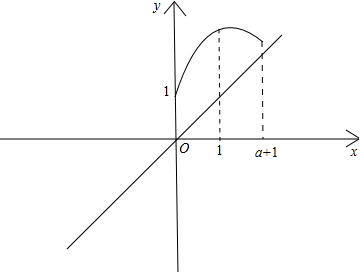 ∴只需f(a+1)>a+1即可;
∴只需f(a+1)>a+1即可;
即$\frac{{e}^{a+1}}{a+2}-a-1>0$在a∈$[0,\frac{1}{2}]$上恒成立,设g(a)=$\frac{{e}^{a+1}}{a+2}-a-1$;
$g′(a)=\frac{{e}^{a+1}(a+1)}{(a+2)^{2}}-1$,g″(a)=$\frac{{e}^{a+1}(a+2)({a}^{2}+2a+2)}{(a+2)^{4}}$>0;
∴g′(a)在[0,$\frac{1}{2}$]上单调递增;
∴$g′(a)≥g′(0)=\frac{e}{4}>0$;
∴g(a)在[0,$\frac{1}{2}$]上单调递增;
∴$g(a)≥g(0)=\frac{e}{2}-1>0$;
即g(a)>0成立;
即f(a+1)>a+1成立;
∴函数y=f(x)的图象总在不等式y>x所表示的平面区域内.
点评 考查根据导数求过曲线上一点切线方程的方法与过程,知道切线的斜率为函数在切点处的导数,直线的点斜式方程,函数极值的定义及求法.能找出y>x表示的平面区域,以及数形结合解题的方法,根据函数导数符号判断函数单调性的方法,以及单调性定义的运用,注意正确求导.

| 日销售量(个) | 10 | 20 | 30 |
| 频数 | 20 | 30 | 50 |
(2)若以频率为概率,其每天的销售量相互独立;
①求6天中大熊猫玩具恰有2天的销售量为30个的概率;
②若每个大熊猫玩具的销售利润为10元,X表示两天的销售利润的和,求X的分布列和数学期望.
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}i$ | D. | -$\frac{5}{2}i$ |

| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
 如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,M是AD的中点,P,Q分别是BM与CD的中点,
如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,M是AD的中点,P,Q分别是BM与CD的中点, 如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.
如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.