题目内容
【题目】已知用“斜二测”画图法画一个水平放置的圆时,所得图形是椭圆,则该椭圆的离心率为_______
【答案】![]()
【解析】
为了简化问题,我们可以设单位圆x+y=1,先求出单位圆直观图的方程(x-y)+8y=1. 画出圆的外切正方形,和椭圆的外切平行四边形,椭圆经过了适当旋转,OC即为椭圆的a,OD即为椭圆的b,根据椭圆上的点到原点的距离最大为a,最小为b,我们可以求出a和b,从而推导出离心率.
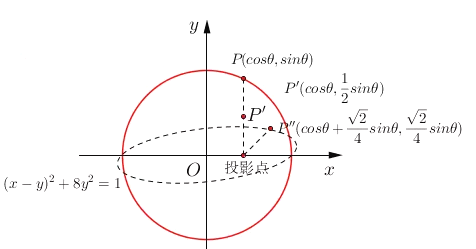
为了简化问题,我们可以设单位圆x+y=1,即圆上的点P(cosθ,sinθ),第一步变换,到它在x轴的投影的距离缩短一半,即![]() (cosθ,0.5sinθ),第二步变换,绕着投影点顺时针旋转45°,即
(cosθ,0.5sinθ),第二步变换,绕着投影点顺时针旋转45°,即![]() (cosθ+
(cosθ+![]() sinθ,
sinθ,![]() sinθ),所以据此得到单位圆的直观图的参数方程为,x=cosθ+
sinθ),所以据此得到单位圆的直观图的参数方程为,x=cosθ+![]() sinθ,y=
sinθ,y=![]() sinθ,θ为参数,消去参数可得方程为,(x-y)+8y=1.
sinθ,θ为参数,消去参数可得方程为,(x-y)+8y=1.
得到单位圆的直观图后,和上面一样,我们画出圆的外切正方形,和椭圆的外切平行四边形,当然就相当完美了!A、B处均与椭圆相切,并且可以轻易发现,椭圆的长轴其实已经不在x轴上了
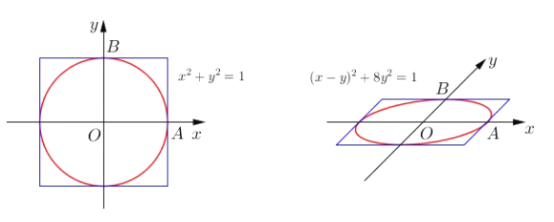
该椭圆经过了适当旋转,OC即为椭圆的a,OD即为椭圆的b,根据椭圆上的点到原点的距离最大为a,最小为b,我们可以求出a和b,从而推导出离心率.
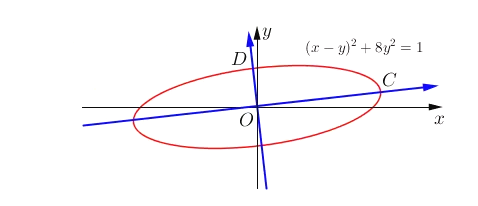
椭圆上的点(cosθ+![]() sinθ,
sinθ,![]() sinθ)到原点的距离的平方为
sinθ)到原点的距离的平方为
![]()
=![]() ,
,
所以![]() ,
,
所以![]()
故答案为:![]()

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目