题目内容
【题目】函数![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域;
上的值域;
(2)是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 递减,并且最大值为1,若存在,求出
递减,并且最大值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)不存在
(2)不存在
【解析】
试题分析:(1)由题意可得,3-2x>0,解不等式可求函数f(x)的定义域,结合函数单调性可求得函数值域;(2)假设存在满足条件的a,由a>0且a≠1可知函数t=3-ax为单调递减的函数,则由复合函数的单调性可知,y=logat在定义域上单调递增,且t=3-ax>0在[1,2]上恒成立,f(1)=1,从而可求a的范围
试题解析:(1)由题意:![]() ,---------------------------2
,---------------------------2
令![]() ,所以
,所以![]() -
-
所以函数![]() 的值域为
的值域为![]() ; ------------------4
; ------------------4
(2)令![]() ,则
,则![]() 在
在![]() 上恒正,
上恒正,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,即
,即![]()
又函数![]() 在
在![]() 递减,
递减,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,即
,即![]() -----7
-----7
又函数![]() 在
在![]() 的最大值为1,
的最大值为1,![]() ,
,
即![]() ,----------10
,----------10 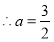 ---------------11
---------------11
![]() 与
与![]() 矛盾,
矛盾,![]() 不存在. ---------------12
不存在. ---------------12

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目