题目内容
16.若函数f(x)=x2+ax+b,a、b∈R的两个零点x1、x2满足x1∈(-1,1),x2∈(2,4),试求a+2b的取值范围.分析 根据函数零点的取值范围,建立不等式关系,利用线性规划的知识即可得到结论.
解答  解:函数f(x)=x2+ax+b,a、b∈R的两个零点x1、x2满足x1∈(-1,1),x2∈(2,4),
解:函数f(x)=x2+ax+b,a、b∈R的两个零点x1、x2满足x1∈(-1,1),x2∈(2,4),
∴$\left\{\begin{array}{l}f(-1)>0\\ f(1)<0\\ f(2)<0\\ f(4)>0\end{array}\right.$,即$\left\{\begin{array}{l}1-a+b>0\\ 1+a+b<0\\ 4+2a+b<0\\ 16+4a+b>0\end{array}\right.$,
作出可行域如图:$\left\{\begin{array}{l}1-a+b=0\\ 16+4a+b=0\end{array}\right.$,可得A(-3,-4),∴a+2b=-11
$\left\{\begin{array}{l}1+a+b=0\\ 16+4a+b=0\end{array}\right.$,解得B(-5,4),∴a+2b=3,
即-11<a+2b<3.
点评 本题主要考查函数的零点,利用一元二次函数和线性规划的知识是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
8.若a+b=m${\;}^{\frac{1}{3}}$,ab=$\frac{1}{6}$m${\;}^{\frac{2}{3}}$(a>b),则a3+b3的值为( )
| A. | 0 | B. | $\frac{m}{2}$ | C. | -$\frac{m}{2}$ | D. | $\frac{3}{2}$m |
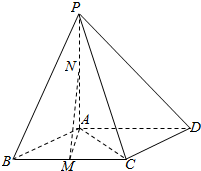 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD点M,N分别是BC,PA的中点,且PA=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD点M,N分别是BC,PA的中点,且PA=PB=2.