题目内容
已知α,β均为锐角,且sin α-sin β=-| 1 |
| 2 |
| 1 |
| 3 |
分析:欲求三角函数cos(α-β)的值,只须求出sin αsin β和cos αcos β,这两个式子可以从已知条件中经过平方得到.
解答:解:∵sin α-sin β=-
,
∴平方得:且sin2α+sin2β-2sin αsin β=
,
∵cos α-cos β=
,平方得:
∴cos2α+cos2β-2cos αcos β=
,
∴两式相加得:2-2cos(α-β)=
.
故填:
.
| 1 |
| 2 |
∴平方得:且sin2α+sin2β-2sin αsin β=
| 1 |
| 4 |
∵cos α-cos β=
| 1 |
| 3 |
∴cos2α+cos2β-2cos αcos β=
| 1 |
| 9 |
∴两式相加得:2-2cos(α-β)=
| 43 |
| 56 |
故填:
| 43 |
| 56 |
点评:本题主要考查两角和与差的余弦函数,研究三角函数的求值问题,通常借助于三角恒等变换,逆向使用三角公式.

练习册系列答案
相关题目
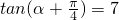 ,
, ,α,β均为锐角.
,α,β均为锐角.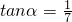 ,
,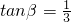 ,α,β均为锐角
,α,β均为锐角 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 ,设
,设 ,
, 均为锐角.
均为锐角. ;
; 的数量积
的数量积 的值.
的值.