题目内容
盒内含有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球，规定取出1个红色球得1分，取出一个白球得0分，取出一个黑球得-1分，现从盒内一次性取3个球．
（1）求取出的三个球得分之和恰为1分的概率
（2）设ξ为取出的3个球中白色球的个数，求ξ分布列和数学期望．
（1）求取出的三个球得分之和恰为1分的概率
（2）设ξ为取出的3个球中白色球的个数，求ξ分布列和数学期望．
（1）记“取出1个红色球，2个白色球”为事件A，“取出2个红色球，1个黑色球”为事件B，
则P（A+B）=P（A）+P（B）=
+
=
（2）ξ可能的取值为0，1，2，3．
P（ξ=0）=
=
，P（ξ=1）=
=
，P（ξ=2）=
=
，P（ξ=3）=
=
ξ的分布列为：
ξ的数学期望Eξ=0×
+1×
+2×
+3×
=1．
则P（A+B）=P（A）+P（B）=
| ||||
|
| ||||
|
| 5 |
| 42 |
（2）ξ可能的取值为0，1，2，3．
P（ξ=0）=
| ||
|
| 5 |
| 21 |
| ||||
|
| 15 |
| 28 |
| ||||
|
| 3 |
| 14 |
| ||
|
| 1 |
| 84 |
ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 21 |
| 15 |
| 28 |
| 3 |
| 14 |
| 1 |
| 84 |
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
的有8人．
的值及甲班学生每天平均学习时间在区间
的人数；
，求
秒且小于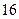
秒认为良好，求该班在这次百米测试中成绩良好的人数；
的概率。
，
，与随机变量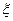
相关的三个概率的值分别是
、
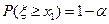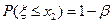和
，则
的最大值为________________．
