题目内容
若海上有A、B、C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC=75°,则B、C间的距离是________海里.
5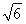
【解析】由正弦定理,知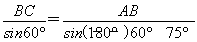 ,解得BC=5
,解得BC=5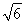 (海里).
(海里).

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
题目内容
若海上有A、B、C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC=75°,则B、C间的距离是________海里.
5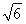
【解析】由正弦定理,知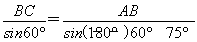 ,解得BC=5
,解得BC=5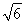 (海里).
(海里).

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案