题目内容
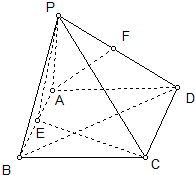 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD于A,E、F分别是AB,PD之中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD于A,E、F分别是AB,PD之中点.(1)求证:AF∥平面PCE.
(2)若二面角P-CD-B为450,求证:平面PCE⊥平面PCD.
分析:(1)要证AF∥平面PCE,只需证明AF与平面PCE 内的一条直线平行即可.设G为PC中点,连接GF,GE,能够证明EAFG为平行四边形,证出AF∥EG后,问题获证.
(2)若二面角P-CD-B为45,可以得出∠PDA=45°,△PDA 为等腰直角三角形,得出AF⊥PD,AF⊥面PDC,再由(1)证得AF∥EG,得出EG⊥面PDC后,即可证出.
(2)若二面角P-CD-B为45,可以得出∠PDA=45°,△PDA 为等腰直角三角形,得出AF⊥PD,AF⊥面PDC,再由(1)证得AF∥EG,得出EG⊥面PDC后,即可证出.
解答: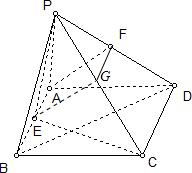 解:(1)设G为PC中点,连接GF,GE
解:(1)设G为PC中点,连接GF,GE
∵E、F分别是AB,PD之中点,
∴FG∥CD,FG=
CD.EA∥CD,EA=
CD.
∴EAFG为平行四边形,
∴AF∥EG,又AF?平面PCE.EG?平面PCE.
∴AF∥平面PCE.
(2)∵PA⊥平面ABCD,
∴PA⊥CD,又AD⊥CD,CD⊥面PAD,
∴CD⊥DP,∠PDA为二面角P-CD-B的平面角,
∴∠PDA=45°,可得△PDA 为等腰直角三角形.
又 F是PD之中点,
∴AF⊥PD,又CD⊥AF,
∴AF⊥面PDC,由(1)证得AF∥EG,所以EG⊥面PDC,.
又EG?平面PCE,
∴平面PCE⊥平面PCD.
 解:(1)设G为PC中点,连接GF,GE
解:(1)设G为PC中点,连接GF,GE∵E、F分别是AB,PD之中点,
∴FG∥CD,FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EAFG为平行四边形,
∴AF∥EG,又AF?平面PCE.EG?平面PCE.
∴AF∥平面PCE.
(2)∵PA⊥平面ABCD,
∴PA⊥CD,又AD⊥CD,CD⊥面PAD,
∴CD⊥DP,∠PDA为二面角P-CD-B的平面角,
∴∠PDA=45°,可得△PDA 为等腰直角三角形.
又 F是PD之中点,
∴AF⊥PD,又CD⊥AF,
∴AF⊥面PDC,由(1)证得AF∥EG,所以EG⊥面PDC,.
又EG?平面PCE,
∴平面PCE⊥平面PCD.
点评:本题考查空间平行和垂直的位置关系的判定,二面角的定义及度量,考查空间想象能力,推理论证能力、转化能力.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=