题目内容
设函数
，若对于任意的
都有
成立，则实数
的值为 ▲
4 解析:本小题考查函数单调性的综合运用.若x=0,则不论a取何值,f(x)≥0显然成立;
当x＞0即x∈(0,1］时,f(x)=ax3-3x+1≥0可化为a≥,
设g(x)=,则g′(x)=,
所以g(x)在区间(0,］上单调递增,在区间［
,1］上单调递减.
因此g(x)max=g(
)=4,从而a≥4;
当x＜0即x∈［-1,0)时,f(x)=ax3-3x+1≥0可化为a≤
,
g(x)在区间［-1,0)上单调递增,
因此g(x)min=g(-1)=4,从而a≤4,综上a=4.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
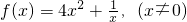
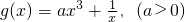，若对于任意的x∈（0，2]，都有f（x）≥g（x）成立，求a的取值范围．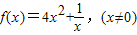
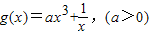在
处取得极值2 ， 
的解析式；
上除原点O外的任意一点，过OA的中点且垂直于
轴的直线交曲线于点B，试问：是否存在这样的点A,使得曲线在点B处的切线与OA平行？若存在，求出点A的坐标；若不存在，说明理由；
，若对于任意
的，总存在
，使得
，求实数
的取值范围。
在
处取得极值2 ，
的解析式；
上除原点O外的任意一点，过OA的中点且垂直于
轴的直线交曲线于点B，试问：是否存在这样的点A,使得曲线在点B处的切线与OA平行？若存在，求出点A的坐标；若不存在，说明理由；
，若对于任意
的，总存在
，使得
，求实数
的取值范围。
，若对于任意的x∈（0，2]，都有f（x）≥g（x）成立，求a的取值范围．