题目内容
已知函数![]() 在
在![]() 处取得极值2 ,
处取得极值2 ,
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设A是曲线![]() 上除原点O外的任意一点,过OA的中点且垂直于
上除原点O外的任意一点,过OA的中点且垂直于![]() 轴的直线交曲线于点B,试问:是否存在这样的点A,使得曲线在点B处的切线与OA平行?若存在,求出点A的坐标;若不存在,说明理由;
轴的直线交曲线于点B,试问:是否存在这样的点A,使得曲线在点B处的切线与OA平行?若存在,求出点A的坐标;若不存在,说明理由;
(Ⅲ)设函数![]() ,若对于任意
,若对于任意![]() 的,总存在
的,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(I)
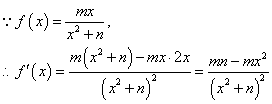
.………2分
又![]() 在
在![]() 处取得极值2.
处取得极值2.
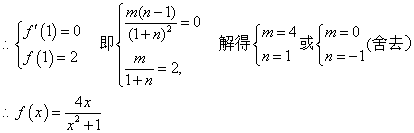
………………4分
(Ⅱ)由(I)得
假设存在满足条件的点A,且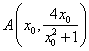 ,则
,则![]() ………………6分
………………6分
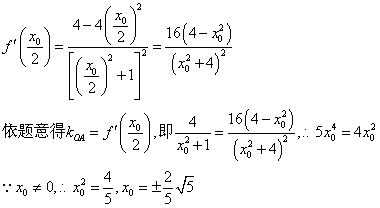 ………………8分
………………8分
所以存在满足条件的点A,此时点A是坐标为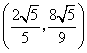 或
或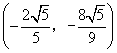 ……9分
……9分
(Ⅲ)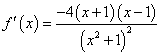 ,令
,令![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| 1 |
|
|
| - | 0 | + | 0 | - |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
![]()
![]() 在
在![]() 处取得极小值
处取得极小值![]() ,在
,在![]() 处取得极大值
处取得极大值![]()
又![]() 时,
时,![]() ,
,![]() 的最小值为-2………………………11分
的最小值为-2………………………11分
![]() 对于任意的
对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() 最小值不大于-2
最小值不大于-2
又![]()
当 ![]() 时,
时,![]() 的最小值为
的最小值为![]() ,由
,由![]()
得![]() ………………………………………12分
………………………………………12分
当![]() 时,
时,![]() 最小值为
最小值为![]() ,由
,由![]() ,得
,得![]()
当![]() 时,
时,![]() 的最小值为
的最小值为![]()
由![]() ,得
,得![]() 或
或![]() ,又
,又![]() ,
,
所以此时![]() 不存在.………………………………13分
不存在.………………………………13分
综上,![]() 的取值范围是
的取值范围是![]() ………………………14分
………………………14分
(Ⅲ)解法二:解法过程同上可求出f(x)的最小值为-2
![]() 对于任意的
对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() 有解 ,即
有解 ,即![]() 在
在![]() 有解
有解
设![]()

所以当![]() 或
或![]() 时,
时,![]()
(Ⅲ)解法三:解法过程同上可求出f(x)的最小值为-2
![]() 对于任意的
对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() 有解.
有解.

综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 在
在 处取得极值.
处取得极值. ;
; ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围. =
= 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 在
在 处取得极值。
处取得极值。 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 为实数。
为实数。 在
在 处取得极值,求
处取得极值,求 的值;
的值;
 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。 在
在 处取得极值.
处取得极值. 的值;[来源:学+科+网]
的值;[来源:学+科+网] 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数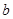 的取值范围.
的取值范围.