题目内容
已知 的展开式的二项式系数之和为
的展开式的二项式系数之和为 ,且展开式中含
,且展开式中含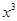 项的系数为
项的系数为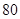 .⑴求
.⑴求 的值;⑵求
的值;⑵求 展开式中含
展开式中含 项的系数.
项的系数.
(1)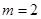 ,
,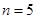 ;(2)
;(2)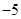 .
.
解析试题分析:(1)二项式系数之和为: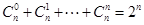 ,令
,令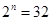 易求得
易求得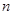 ,其次利用二项展开式的通项公式中令
,其次利用二项展开式的通项公式中令 ,易求得
,易求得 ;(2)在前小题已求得的
;(2)在前小题已求得的 的基础上,要求
的基础上,要求 展开式中求特定项(含
展开式中求特定项(含 项)的系数,只需把两个二项式展开,对于
项)的系数,只需把两个二项式展开,对于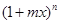 展开式中的常数项与
展开式中的常数项与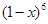 展开式中的
展开式中的 项的系数乘,一次项系数与其一次项系数乘,二次项系数与其常数项乘,再把所得值相加即为所求.
项的系数乘,一次项系数与其一次项系数乘,二次项系数与其常数项乘,再把所得值相加即为所求.
试题解析:⑴由题意,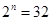 ,则
,则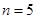 ,由通项公式
,由通项公式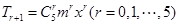 ,则
,则 ,所以
,所以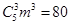 ,所以
,所以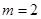 ;⑵本小题即求
;⑵本小题即求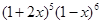 展开式中含
展开式中含 项的系数,
项的系数,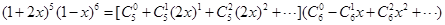
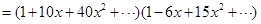 ,所以展开式中含
,所以展开式中含 项的系数为
项的系数为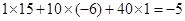 .
.
考点:二项式定理,二项式系数和,利用二项展开式的通项公式求特定项,化归思想.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 的展开式中常数项为 。
的展开式中常数项为 。 展开式的二项式系数和为512,且
展开式的二项式系数和为512,且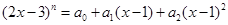
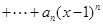 .
.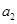 的值; (2)求
的值; (2)求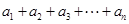 的值.
的值.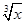 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-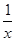 )2n的展开式中:
)2n的展开式中: )7展开式中x3的系数为 .
)7展开式中x3的系数为 . 的展开式中的常数项是_____________.
的展开式中的常数项是_____________.