题目内容
已知函数f（x）=
若数列{an}满a1=
，an+1=f（an），n∈N*，则a2006+a2009+a2010= ．
【答案】分析：先要通过a1求出a2，a3，a4，a5，a6，a7，…从中找出数列的规律来．从而求出a2006+a2009+a2010
解答：解；∵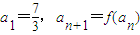
，∴
，
∴
，
∴
，
∴
，
，…
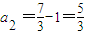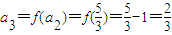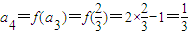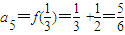由此可得，a4=a7=a10=…，a5=a8=a11=…，a6=a9=a12=…
∴a2006=a5，a2009=a5，a2010=a6
∴
，
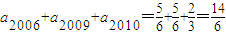故答案为：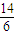
．
点评：此题考查函数周期性．处理时，必须从数列的前几项找出规律来，从而发现数列的周期．
解答：解；∵
，∴，∴
，∴
，∴
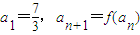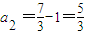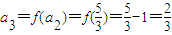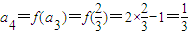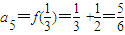，，…由此可得，a4=a7=a10=…，a5=a8=a11=…，a6=a9=a12=…
∴a2006=a5，a2009=a5，a2010=a6
∴
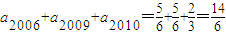，故答案为：
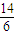．点评：此题考查函数周期性．处理时，必须从数列的前几项找出规律来，从而发现数列的周期．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、命题：“已知函数f（x），若f（x+1）与f（x-1）均为奇函数，则f（x）为奇函数，”为直命题 | B、“x＞1”是“|x|＞1”的必要不充分条件 | C、若“p且q”为假命题，则p，q均为假命题 | D、命题p：”?x∈R，使得x2+x+1＜0”，则?p：”?x∈R，均有x2+x+1≥0” |
，若f（a）=
，则实数a的值为（ ）
