题目内容
【题目】如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2 , |AB|=4,|F1F2|=2 ![]() ,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
(Ⅰ)求椭圆E的离心率;
(Ⅱ)若m>0,设直线AD、BC的斜率分别为k1、k2 , 求 ![]() 的取值范围.
的取值范围.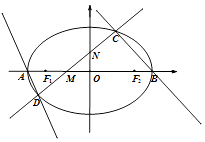
【答案】解:(Ⅰ)由 ![]() ,可知
,可知 ![]() 即椭圆方程为
即椭圆方程为 ![]()
离心率为 ![]()
(Ⅱ)设D(x1,y1),C(x2,y2)易知 ![]() .
.
由 ![]() 消去y整理得:(1+4k2)x2+8kmx+4m2﹣4=0,
消去y整理得:(1+4k2)x2+8kmx+4m2﹣4=0,
由△>04k2﹣m2+1>0即m2<4k2+1, ![]()
且|CM|=|DN|即 ![]() 可知
可知 ![]() ,即
,即 ![]() ,解得
,解得 ![]() .
.
由题知,点M、F1的横坐标 ![]() ,有
,有 ![]() ,
,
易知 ![]() 满足m2<2,
满足m2<2,
即 ![]() ,则
,则 ![]()
【解析】(Ⅰ)由 ![]() ,求出a,c,然后求解椭圆的离心率.(Ⅱ)设D(x1,y1),C(x2,y2)通过
,求出a,c,然后求解椭圆的离心率.(Ⅱ)设D(x1,y1),C(x2,y2)通过 ![]() ,结合△>0推出m2<4k2+1,利用韦达定理|CM|=|DN|.求出直线的斜率,然后表示出
,结合△>0推出m2<4k2+1,利用韦达定理|CM|=|DN|.求出直线的斜率,然后表示出 ![]() ,然后求解它的范围即可.
,然后求解它的范围即可.

练习册系列答案
相关题目