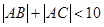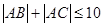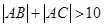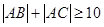题目内容
设直线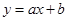 与双曲线
与双曲线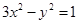 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点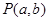 的轨迹方程.
的轨迹方程.
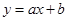 与双曲线
与双曲线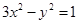 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点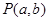 的轨迹方程.
的轨迹方程.2y2-x2=1(x2<3).
试题分析:将直线与双曲线方程联立,消去y(或x),得到关于x的一元二次方程。由题意知方程有两根,故二次项系数不为0,且判别式大于0,解出a的范围,即所求轨迹方程的定义域。根据韦达定理得到两根之和,两根之积(整体计算比计算出两个根要简单)。根据且以AB为直径的圆过原点,可得直线AO和直线BO垂直,可利用斜率之积等于
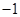 列式计算,但这种情况需对斜率存在与否进行讨论。为了省去讨论的麻烦可用向量问题来解决。详见解析。
列式计算,但这种情况需对斜率存在与否进行讨论。为了省去讨论的麻烦可用向量问题来解决。详见解析。试题解析: 解:联立直线与双曲线方程得
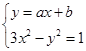 ,消去y得:(a2-3)x2+2abx+b2+1=0.
,消去y得:(a2-3)x2+2abx+b2+1=0.∵直线与双曲线交于A、B两点,∴
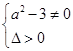 ⇒a2<3.
⇒a2<3.设A(x1,y1),B(x2,y2)则x1+x2=
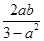 ,x1·x2=
,x1·x2=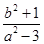 .
.由
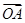 ⊥
⊥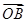 得x1x2+y1y2=0,又y1·y2=(ax1+b)(ax2+b)=a2x1x2+ab(x1+x2)+b2,
得x1x2+y1y2=0,又y1·y2=(ax1+b)(ax2+b)=a2x1x2+ab(x1+x2)+b2,∴有
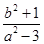 +a2·
+a2·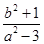 -
-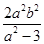 +b2=0.
+b2=0.化简得:a2-2b2=-1.故P点(a,b)的轨迹方程为2y2-x2=1(x2<3).

练习册系列答案
相关题目
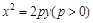 ,定点M(0,5),直线
,定点M(0,5),直线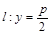 与
与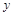 轴交于点F,O为原点,若以OM为直径的圆恰好过
轴交于点F,O为原点,若以OM为直径的圆恰好过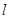 与抛物线C的交点.
与抛物线C的交点.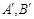 ,求证: 抛物线C分别过
,求证: 抛物线C分别过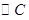 :
: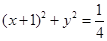 ,
,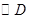 :
: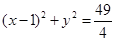 .动点P与
.动点P与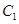 的方程;
的方程;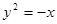 与直线
与直线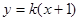 相交于A、B 两点.
相交于A、B 两点.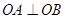 ;
;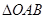 的面积等于
的面积等于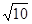 时,求
时,求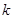 的值.
的值.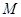 :
: 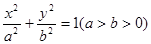 的离心率为
的离心率为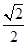 ,点
,点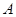 (
(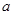 ,0),
,0),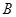 (0,
(0,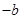 )原点
)原点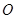 到直线
到直线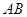 的距离为
的距离为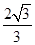 。
。
 为(
为(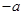 ,0),点
,0),点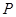 在椭圆
在椭圆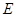 在直线
在直线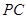 上,若直线
上,若直线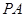 的方程为
的方程为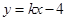 ,且
,且 ,试求直线
,试求直线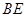 的方程.
的方程.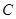 的方程为
的方程为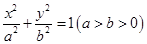 ,双曲线
,双曲线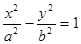 的两条渐近线为
的两条渐近线为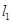 、
、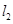 .过椭圆
.过椭圆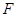 作直线
作直线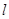 ,使
,使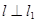 ,又
,又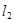 交于点
交于点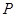 ,设
,设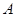 、
、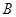 .
.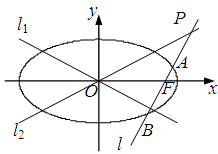
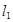 与
与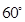 ,且双曲线的焦距为
,且双曲线的焦距为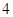 ,求椭圆
,求椭圆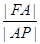 的最大值.
的最大值. 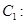
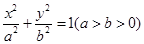 的离心率为
的离心率为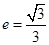 ,直线
,直线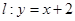 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆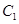 的短半轴长为半径的圆
的短半轴长为半径的圆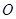 相切.
相切.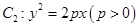 与椭圆
与椭圆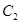 有公共焦点,设
有公共焦点,设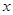 轴交于点
轴交于点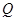 ,不同的两点
,不同的两点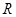 、
、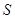 在
在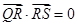 ,求
,求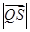 的取值范围.
的取值范围. 的椭圆过点
的椭圆过点
 与该椭圆交于P,Q两点,满足直线
与该椭圆交于P,Q两点,满足直线 的斜率依次成等比数列,
的斜率依次成等比数列, 面积的取值范围.
面积的取值范围.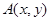 满足
满足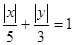 ,
,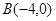 ,
,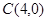 ,则一定有( )
,则一定有( )