Question

【题目】在棱长为2的正方体中，点M是对角线上的点（点M与A、不重合），则下列结论正确的个数为（ ）

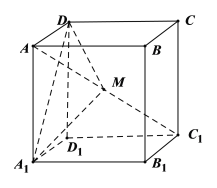
①存在点M，使得平面平面；

②存在点M，使得平面；

③若的面积为S，则；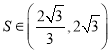

④若、分别是在平面与平面的正投影的面积，则存在点M，使得.

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

平面与平面为同一平面,证明平面即可判断①；由证明平面平面判断②；连接交于点O,当时可得,利用相似可得,进而求得的最小面积,即可判断③；分别判断点从的中点向着点A运动的过程中,、的范围,进而判断④.

连接,,

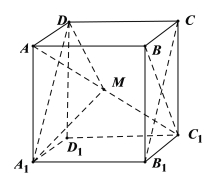
设平面与对角线交于M,由,可得平面,即平面,所以存在点M,使得平面平面,所以①正确；

连接,,

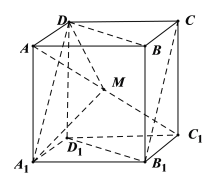
由,,利用平面与平面平行的判定,可证得平面平面,设平面与交于M,可得平面,所以②正确；

连接交于点O,过O点作,

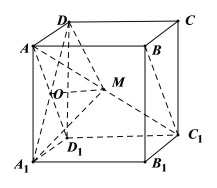
在正方体中,平面,所以,所以OM为异面直线与的公垂线,根据,所以,即,

所以的最小面积为,

所以若的面积为S,则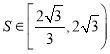,所以③不正确；

在点从的中点向着点A运动的过程中,从1减少趋向于0,即,从0增大到趋向于2,即,在此过程中,必存在某个点使得,所以④是正确的,

综上可得①②④是正确的,

故选:C