题目内容
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为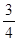 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为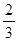 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分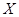 的分布列及数学期望
的分布列及数学期望 ;
;
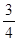 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为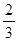 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分
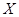 的分布列及数学期望
的分布列及数学期望 ;
;(I)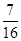 .
.
(II)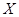 的分布列是
的分布列是
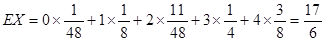 .
.
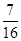 .
. (II)
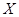 的分布列是
的分布列是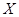 | 0 | 1 | 2 | 3 | 4 |
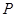 | 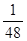 | 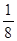 | 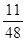 | 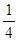 | 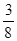 |
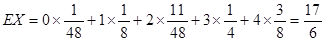 .
.试题分析:(I)此类题的一般解法是,标记事件,计算概率,注意到记:“该射手恰好命中两次”为事件
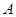 ,“该射手第一次射击甲靶命中”为事件
,“该射手第一次射击甲靶命中”为事件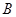 ,“该射手第二次射击甲靶命中”为事件
,“该射手第二次射击甲靶命中”为事件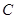 ,“该射手射击乙靶命中”为事件
,“该射手射击乙靶命中”为事件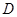 .可得,
.可得,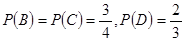 ,
,进一步利用
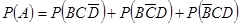
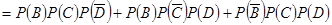
计算即得.
(II)注意到
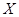 的所有可能取值为0,1,2,3,4.利用独立事件同时发生的概率计算公式可得.细心计算是关键.
的所有可能取值为0,1,2,3,4.利用独立事件同时发生的概率计算公式可得.细心计算是关键.试题解析:(I)记:“该射手恰好命中两次”为事件
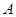 ,“该射手第一次射击甲靶命中”为事件
,“该射手第一次射击甲靶命中”为事件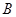 ,“该射手第二次射击甲靶命中”为事件
,“该射手第二次射击甲靶命中”为事件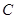 ,“该射手射击乙靶命中”为事件
,“该射手射击乙靶命中”为事件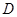 .
.由题意知,
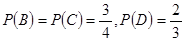 ,
,所以
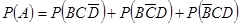
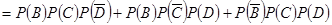
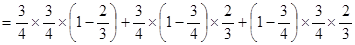
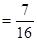 . 6分
. 6分(II)根据题意,
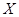 的所有可能取值为0,1,2,3,4.
的所有可能取值为0,1,2,3,4. ,
,
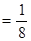 .
.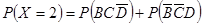
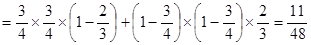 ,
,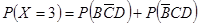
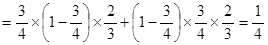 ,
,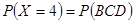
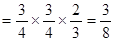 , 11分
, 11分故
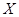 的分布列是
的分布列是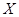 | 0 | 1 | 2 | 3 | 4 |
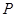 | 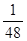 | 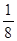 | 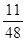 | 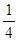 | 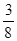 |
所以
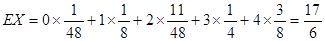 . 14分
. 14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生. ,求
,求 .
. 的概率分布列及期望.
的概率分布列及期望. 为取得红球的个数.
为取得红球的个数.  .
.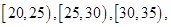
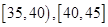 .
.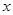 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在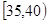 岁的人数;
岁的人数;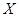 ,求
,求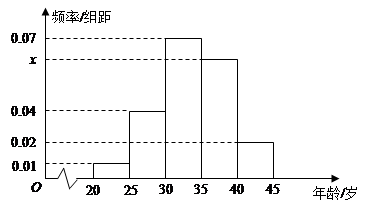
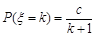 (k=0,1,2,3),则
(k=0,1,2,3),则 .
.  ,求
,求


 ,且
,且 ,则实数
,则实数 的值为 ( )
的值为 ( )