题目内容
已知函数f(x)的定义域为(0,+∞),若y= 在(0,+∞)上为增函数,则称f(x) 为“一阶比增函数”.
在(0,+∞)上为增函数,则称f(x) 为“一阶比增函数”.
(Ⅰ) 若f(x)=ax2+ax是“一阶比增函数”,求实数a的取值范围;
(Ⅱ) 若f(x)是“一阶比增函数”,求证:?x1,x2∈(0,+∞),f(x1)+f(x2)<f(x1+x2);
(Ⅲ)若f(x)是“一阶比增函数”,且f(x)有零点,求证:f(x)>2013有解.
解:(I)由题意得y=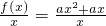 =ax+a在(0,+∞)是增函数,
=ax+a在(0,+∞)是增函数,
由一次函数性质知:当a>0时,y=ax+a在(0,∞)上是增函数,
∴a>0.
(Ⅱ)∵f(x)是“一阶比增函数”,即 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
又?x1,x2∈(0,+∞),有x1<x1+x2,x2<x1+x2,
∴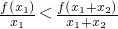 ,
, ,
,
∴ ,
,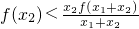 ,
,
∴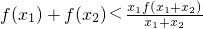 +
+ =f(x1+x2).
=f(x1+x2).
(Ⅲ)设f(x0)=0,其中x0>0.
因为f(x)是“一阶比增函数”,所以当x>x0时,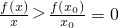 .
.
法一:取t∈(0,+∞),满足f(t)>0,记f(t)=m.
由(Ⅱ)知f(2t)>2m,同理f(4t)>2f(2t)>4m,f(8t)>2f(4t)>8m.
所以一定存在n∈N*,使得f(2nt)>2nm>2013,
所以f(x)>2013 一定有解.
法二:取t∈(0,+∞),满足f(t)>0,记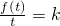 .
.
因为当x>t时,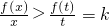 ,所以f(x)>kx对x>t成立.
,所以f(x)>kx对x>t成立.
只要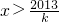 ,则有f(x)>kx>2013,
,则有f(x)>kx>2013,
所以f(x)>2013 一定有解.
分析:(Ⅰ)利用“一阶比增函数”的意义及一次函数的单调性即可得出;
(Ⅱ)利用“一阶比增函数”的意义及增函数的定义即可证明;
(Ⅲ)利用“一阶比增函数”的意义和(Ⅱ)的结论即可证明.
点评:正确“一阶比增函数”的意义及增函数的定义及利用已经证明过的结论是解题的关键.
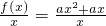 =ax+a在(0,+∞)是增函数,
=ax+a在(0,+∞)是增函数,由一次函数性质知:当a>0时,y=ax+a在(0,∞)上是增函数,
∴a>0.
(Ⅱ)∵f(x)是“一阶比增函数”,即
 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,又?x1,x2∈(0,+∞),有x1<x1+x2,x2<x1+x2,
∴
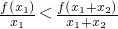 ,
, ,
,∴
 ,
,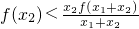 ,
,∴
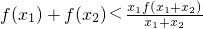 +
+ =f(x1+x2).
=f(x1+x2).(Ⅲ)设f(x0)=0,其中x0>0.
因为f(x)是“一阶比增函数”,所以当x>x0时,
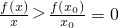 .
.法一:取t∈(0,+∞),满足f(t)>0,记f(t)=m.
由(Ⅱ)知f(2t)>2m,同理f(4t)>2f(2t)>4m,f(8t)>2f(4t)>8m.
所以一定存在n∈N*,使得f(2nt)>2nm>2013,
所以f(x)>2013 一定有解.
法二:取t∈(0,+∞),满足f(t)>0,记
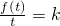 .
.因为当x>t时,
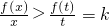 ,所以f(x)>kx对x>t成立.
,所以f(x)>kx对x>t成立.只要
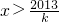 ,则有f(x)>kx>2013,
,则有f(x)>kx>2013,所以f(x)>2013 一定有解.
分析:(Ⅰ)利用“一阶比增函数”的意义及一次函数的单调性即可得出;
(Ⅱ)利用“一阶比增函数”的意义及增函数的定义即可证明;
(Ⅲ)利用“一阶比增函数”的意义和(Ⅱ)的结论即可证明.
点评:正确“一阶比增函数”的意义及增函数的定义及利用已经证明过的结论是解题的关键.

练习册系列答案
相关题目
