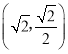题目内容
【题目】已知椭圆
：
，长半轴长与短半轴长的差为
，离心率为
．
（1）求椭圆的标准方程；
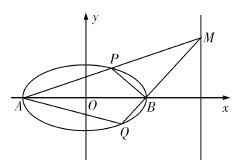
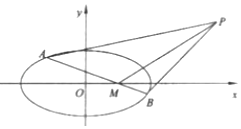
（2）若在
轴上存在点
，过点的直线
分别与椭圆相交于
、
两点，且
为定值，求点的坐标．
【答案】(1) 
(2) 
【解析】
（1）由题意可得：a﹣b
，
，a2＝b2+c2．联立解得：a，c，b．可得椭圆C的标准方程．
（2）设M（t，0），P（x1，y1），Q（x2，y2）．分类讨论：①当直线l的斜率不为0时，设直线l的方程为：x＝my+t．与椭圆方程联立化为：（3m2+4）y2+6mty+3t2﹣12＝0．△＞0．可得|PM|2
（1+m2）
，同理可得：|PQ|2＝（1+m2）
．把根与系数的关系代入
，化简整理可得．②当直线l的斜率为0时，设P（2，0），Q（﹣2，0）．|PM|＝|t+2|，|QM|＝|2﹣t|．代入同理可得结论．
（1）由题意可得：
，
，
．
联立解得：
，
，
，∴椭圆
的标准方程为：.
（2）设
，
，
．
①当直线
的斜率不为0时，设直线的方程为：
．
联立
，化为：
．
．
∴
，
．
，同理可得：
．
∴
.
∵
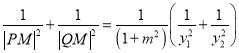
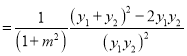
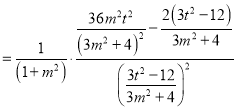
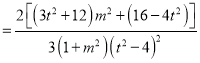为定值，∴必然有
，解得
．
此时
为定值，．
②当直线的斜率为0时，设
，
．
，
．
此时
，把
代入可得：为定值．
综上①②可得：为定值，．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
【题目】随着“互联网+交通”模式的迅猛发展，“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度，随机调查了200名用户，得到用户的满意度评分，现将评分分为5组，如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
（1）求表格中的
，
，
的值；
（2）估计用户的满意度评分的平均数；
（3）若从这200名用户中随机抽取50人，估计满意度评分高于6分的人数为多少？
