题目内容
已知下列命题命题:①椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
分析:①根据a,b,c成等比数列得出a,b,c的关系,进而可求得c关于a的表达式,进而根据 e=
求得e.
②由双曲线的标准方程,则可表示出其渐近线的方程,根据两条直线垂直,推断出其斜率之积为-1进而求得a和b的关系,进而根据c=
求得a和c的关系,则双曲线的离心率可得.
③找出正方体中的四面体的各种图形,例如侧棱垂直底面直角三角形的四面体即可判断③的正误;
④用几何概型判断即可.
| c |
| a |
②由双曲线的标准方程,则可表示出其渐近线的方程,根据两条直线垂直,推断出其斜率之积为-1进而求得a和b的关系,进而根据c=
| a2+b2 |
③找出正方体中的四面体的各种图形,例如侧棱垂直底面直角三角形的四面体即可判断③的正误;
④用几何概型判断即可.
解答:解:①已知a,b,c成等比数列,∴ac=b2,椭圆的离心率 e=
,故正确;
 ②双曲线x2-y2=a2(a>0),则双曲线的渐近线方程为y=±x
②双曲线x2-y2=a2(a>0),则双曲线的渐近线方程为y=±x
∴两条渐近线互相垂直,
∵a2=b2,
∴c=
=
a
∴e=
=
,故正确;
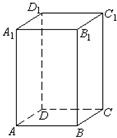
③如四面体B1ABD;故正确;
④概率应为1-
,故错.
故答案是①②③.
| ||
| 2 |
 ②双曲线x2-y2=a2(a>0),则双曲线的渐近线方程为y=±x
②双曲线x2-y2=a2(a>0),则双曲线的渐近线方程为y=±x∴两条渐近线互相垂直,
∵a2=b2,
∴c=
| a2+b2 |
| 2 |
∴e=
| c |
| a |
| 2 |
③如四面体B1ABD;故正确;
④概率应为1-
| π |
| 4 |
故答案是①②③.
点评:本题主要考查了椭圆的基本性质,考查了双曲线的简单性质.解答关键是学生转化和化归思想和对圆锥曲线的基础知识的把握程度.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目