题目内容
已知下列命题:①若向量a∥b,b∥c,则a∥c;②若|a|>|b|,则a>b;③若a•b=0,则a=0或b=0;④在△ABC中,若
•
<0,则△ABC是钝角三角形;⑤(a•b)•c=a•(b•c)、其中正确命题的个数是( )
| AB |
| CA |
| A、0 | B、1 | C、2 | D、3 |
分析:举特例,A
=
时①不正确:根据向量不能比较大小推断出②不正确;通过
⊥
可推断出
•
=0,③不正确.④根据向量的数量积的计算求得cosA>0,A为锐角.根据向量的性质推断出⑤不正确.
| b |
| 0 |
| a |
| b |
| a |
| b |
解答:解:A
=
时①不正确;
向量不能比较大小,②不正确;
⊥
?
•
=0,③不正确;
•
=
•(-
)=-
•
=-|
|•|
|cos∠A<0?cos∠A>0?∠A为锐角,不能判断△ABC的形状,
④不正确;
(
•
)•
≠
•(
•
),⑤不正确.
故选A
| b |
| 0 |
向量不能比较大小,②不正确;
| a |
| b |
| a |
| b |
| AB |
| CA |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
④不正确;
(
| a |
| b |
| c |
| a |
| b |
| c |
故选A
点评:本题主要考查了三角形的形状的判断,向量的平行性质以及向量的数量积.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 个单位即可得到函数
个单位即可得到函数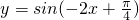 (x∈R)的图象其中真命题是________(只写序号)
(x∈R)的图象其中真命题是________(只写序号) 个单位即可得到函数
个单位即可得到函数 (x∈R)的图象其中真命题是 (只写序号)
(x∈R)的图象其中真命题是 (只写序号)