题目内容
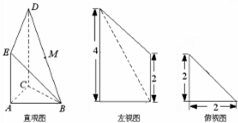 (2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)求证:EM∥平面ABC;
(2)求出该几何体的体积;
(3)试问在平面ACDE上是否存在点N,使MN⊥平面BDE?若存在,确定点N的位置;若不存在,说明理由.
分析:(1)取BC的中点G,利用三角形中位线的性质,可得AGME为平行四边形,从而可得EM∥AG,利用线面平行的判定,可得EM∥平面ABC;
(2)证明AB⊥平面ACDE,可得几何体B-ACDE的高h=AB=2,从而可求VB-ACDE;
(3)利用MN⊥平面BDE,可得
,从而可求存在点N,使MN⊥平面BDE.
(2)证明AB⊥平面ACDE,可得几何体B-ACDE的高h=AB=2,从而可求VB-ACDE;
(3)利用MN⊥平面BDE,可得
|
解答: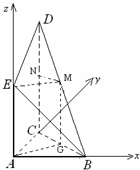 (1)证明:取BC的中点G,连EM,MG,AG
(1)证明:取BC的中点G,连EM,MG,AG
∵M为DB中点,∴MG∥DC且MG=
DC
∴MG平行且等于AE,∴AGME为平行四边形,∴EM∥AG
又EM?平面ABC,AG?平面ABC,∴EM∥平面ABC …(4分)
(2)解:∵EA⊥平面ABC,∴EA⊥AB,
又AB⊥AC,AC∩EA=A,∴AB⊥平面ACDE
∴几何体B-ACDE的高h=AB=2,又S梯形ACDE=6
∴VB-ACDE=
Sh=4 …(8分)
(3)解:如图建立空间坐标系A-xyz,则B(2,0,0),C(0,2,0),E(0,0,2),D(0,2,4),M(1,1,2),设 N(0,y,z),
=(-1,y-1,z-2),
=(-2,0,2),
=(-2,2,4)…(9分)
∵MN⊥平面BDE,∴
,∴
,∴
…(11分)
∴在平面ACDE上是存在点N(0,2,1),使MN⊥平面BDE …(12分)
 (1)证明:取BC的中点G,连EM,MG,AG
(1)证明:取BC的中点G,连EM,MG,AG∵M为DB中点,∴MG∥DC且MG=
| 1 |
| 2 |
∴MG平行且等于AE,∴AGME为平行四边形,∴EM∥AG
又EM?平面ABC,AG?平面ABC,∴EM∥平面ABC …(4分)
(2)解:∵EA⊥平面ABC,∴EA⊥AB,
又AB⊥AC,AC∩EA=A,∴AB⊥平面ACDE
∴几何体B-ACDE的高h=AB=2,又S梯形ACDE=6
∴VB-ACDE=
| 1 |
| 3 |
(3)解:如图建立空间坐标系A-xyz,则B(2,0,0),C(0,2,0),E(0,0,2),D(0,2,4),M(1,1,2),设 N(0,y,z),
| MN |
| BE |
| BD |
∵MN⊥平面BDE,∴
|
|
|
∴在平面ACDE上是存在点N(0,2,1),使MN⊥平面BDE …(12分)
点评:本题考查线面平行,考查几何体的体积计算,考查线面垂直,考查空间向量的运用,掌握线面平行的判定,正确运用空间向量是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2012•上饶一模)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=a,E是PC的中点,作EF⊥PB交PB于点F.
(2012•上饶一模)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=a,E是PC的中点,作EF⊥PB交PB于点F.