题目内容
（2012•上饶一模）如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC=a，E是PC的中点，作EF⊥PB交PB于点F．（Ⅰ）证明：PA∥平面EDB；
（Ⅱ）求三棱锥P-DEF的体积．
分析：（I）连接AC，AC交BD于O．连接EO．根据正方形的性质，得EO是△PAC的中位线，得PA∥EO，从而得到PA∥平面EDB；
（II）过F点作FG⊥PC于G，可得FG⊥平面PDE，FG是点F到平面PDE的距离．等腰Rt△PDC中，算出PE长和△PED的面积，再利用三角形相似算出PF和FG的长，最后用锥体体积公式，可算出三棱锥P-DEF的体积．
（II）过F点作FG⊥PC于G，可得FG⊥平面PDE，FG是点F到平面PDE的距离．等腰Rt△PDC中，算出PE长和△PED的面积，再利用三角形相似算出PF和FG的长，最后用锥体体积公式，可算出三棱锥P-DEF的体积．
解答：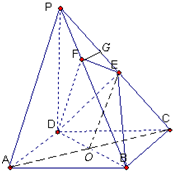
解：（I）连接AC，AC交BD于O．连接EO．
∵底面ABCD是正方形，点O是AC的中点，
∴在△PAC中，EO是中位线，得PA∥EO．
又∵EO?平面EDB，PA?平面EDB，
∴PA∥平面EDB．…（6分）
（II）∵PD=DC=a．PD⊥平面ABCD，E为PC的中点，
∴Rt△PDC中，PC=
=
a，中线PE=
a
Rt△PBD中，PB=
=
a，且S△PDE=
．
∵PD⊥平面ABCD，BC⊆平面ABCD，∴PD⊥BC
又∵BC⊥CD，PD、CD是平面PCD内的相交直线，
∴BC⊥平面PCD，
∴结合PC⊆平面PCD，得BC⊥PC，
又∵EF⊥PB，∴△PFE∽△PCB，
∴
=
，可得PF=
=
=
a．
过F点作FG⊥PC于G，
∵△PBC中，FG、BC都与直线PC垂直，∴FG∥BC，
∴FG⊥平面PCD，即FG⊥平面PDE，得FG是点F到平面PDE的距离，
∵△PFG∽△PBC，得
=
，∴FG=
=
=
．
∴三棱锥P-DEF的体积为VP-DEF=VF-PDE=
•
•
=
．…（12分）
解：（I）连接AC，AC交BD于O．连接EO．∵底面ABCD是正方形，点O是AC的中点，
∴在△PAC中，EO是中位线，得PA∥EO．
又∵EO?平面EDB，PA?平面EDB，
∴PA∥平面EDB．…（6分）
（II）∵PD=DC=a．PD⊥平面ABCD，E为PC的中点，
∴Rt△PDC中，PC=
| PD2+DC2 |
| 2 |
| ||
| 2 |
Rt△PBD中，PB=
| PD2+BD2 |
| 3 |
| a2 |
| 4 |
∵PD⊥平面ABCD，BC⊆平面ABCD，∴PD⊥BC
又∵BC⊥CD，PD、CD是平面PCD内的相交直线，
∴BC⊥平面PCD，
∴结合PC⊆平面PCD，得BC⊥PC，
又∵EF⊥PB，∴△PFE∽△PCB，
∴
| PF |
| PE |
| PC |
| PB |
| PE•PC |
| PB |
| ||||||
|
| ||
| 3 |
过F点作FG⊥PC于G，
∵△PBC中，FG、BC都与直线PC垂直，∴FG∥BC，
∴FG⊥平面PCD，即FG⊥平面PDE，得FG是点F到平面PDE的距离，
∵△PFG∽△PBC，得
| FG |
| BC |
| PF |
| PB |
| BC•PF |
| PB |
a•
| ||||
|
| a |
| 3 |
∴三棱锥P-DEF的体积为VP-DEF=VF-PDE=
| 1 |
| 3 |
| a2 |
| 4 |
| a |
| 3 |
| a3 |
| 36 |
点评：本题给出特殊四棱锥，求证线面平行并求锥体体积，考查了线面平行、线面垂直的判定与性质和锥体体积公式等知识，属于中档题．
练习册系列答案
相关题目