题目内容
(2012•宜宾一模)已知定义在(0,+∞)上的两个函数f(x)=x2-alnx,g(x)=x-a
,且f(x)在x=1处取得极值.
(1)求a的值及函数g(x)的单调区间;
(2)求证:当1<x<e2时,恒有x<
成立.
(3)把g(x)对应的曲线向上平移6个单位后得曲线C1,求C1与f(x)对应曲线C2的交点个数,并说明理由.
| x |
(1)求a的值及函数g(x)的单调区间;
(2)求证:当1<x<e2时,恒有x<
| 2+lnx |
| 2-lnx |
(3)把g(x)对应的曲线向上平移6个单位后得曲线C1,求C1与f(x)对应曲线C2的交点个数,并说明理由.
分析:(1)先根据f'(1)=0求出a的值,然后求出g′(x),最后解g′(x)>0与g′(x)<0,即可求出函数g(x)的单调区间;
(2)先判定2-lnx的符号,欲证x<
,只需证明2x-xlnx<2+lnx,即只需证lnx>
,记F(x)=lnx-
,然后利用导数研究函数的单调性求出函数F(x)的最小值即可证得结论;
(3)由题意知C1:h(x)=x-2
+6,问题转化为G(x)=x2-2lnx-(x-2
+6)=0在(0,+∞)上解的个数,然后利用导数研究函数的单调性,从而可判定解的个数.
(2)先判定2-lnx的符号,欲证x<
| 2+lnx |
| 2-lnx |
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
(3)由题意知C1:h(x)=x-2
| x |
| x |
解答:解:(1)∵f′(x)=2x-
,∴f'(1)=2-a=0,∴a=2.…(2分)
∴g(x)=x-2
.由g′(x)=1-
>0,得x>1;
由g′(x)=1-
<0,得0<x<1.
∴g(x)的单调递减区间是(0,1),单调递增区间是(1,+∞).…(4分)
(2)∵1<x<e2,
∴0<lnx<2,
∴2-lnx>0.
欲证x<
,只需证明2x-xlnx<2+lnx,
即只需证lnx>
.
记F(x)=lnx-
,
则F′(x)=
.
当x>1时,F'(x)>0,
∴F(x)在(1,+∞)上是增函数.
∴F(x)>F(1)=0,
∴F(x)>0,即lnx-
>0.
∴lnx>
.故结论成立. …(8分)
(3)由题意知C1:h(x)=x-2
+6.
问题转化为G(x)=x2-2lnx-(x-2
+6)=0在(0,+∞)上解的个数.…(10分)
G′(x)=2x-2
-1+
=
=
.
由G'(x)>0,得x>1;由G'(x)<0,得0<x<1.
∴G(x)在区间(1,+∞)上单调递增,在区间(0,1)上单调递减.
又G(1)=-4<0,所以G(x)=x2-2lnx-(x-2
+6)=0
在(0,+∞)上有2个解.
即C1与f(x)对应曲线C2的交点个数是2.…(14分)
| a |
| x |
∴g(x)=x-2
| x |
| 1 | ||
|
由g′(x)=1-
| 1 | ||
|
∴g(x)的单调递减区间是(0,1),单调递增区间是(1,+∞).…(4分)
(2)∵1<x<e2,
∴0<lnx<2,
∴2-lnx>0.
欲证x<
| 2+lnx |
| 2-lnx |
即只需证lnx>
| 2(x-1) |
| x+1 |
记F(x)=lnx-
| 2(x-1) |
| x+1 |
则F′(x)=
| (x-1)2 |
| x(x+1)2 |
当x>1时,F'(x)>0,
∴F(x)在(1,+∞)上是增函数.
∴F(x)>F(1)=0,
∴F(x)>0,即lnx-
| 2(x-1) |
| x+1 |
∴lnx>
| 2(x-1) |
| x+1 |
(3)由题意知C1:h(x)=x-2
| x |
问题转化为G(x)=x2-2lnx-(x-2
| x |
G′(x)=2x-2
| 1 |
| x |
| 1 | ||
|
2x2-2-x+
| ||
| x |
(
| ||||||
| x |
由G'(x)>0,得x>1;由G'(x)<0,得0<x<1.
∴G(x)在区间(1,+∞)上单调递增,在区间(0,1)上单调递减.
又G(1)=-4<0,所以G(x)=x2-2lnx-(x-2
| x |
在(0,+∞)上有2个解.
即C1与f(x)对应曲线C2的交点个数是2.…(14分)
点评:本题主要考查了利用导数研究函数的极值,以及函数的单调性和图象交点问题,同时考查了转化的思想,属于中档题.

练习册系列答案
相关题目
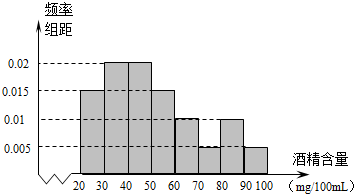 (2012•宜宾一模)《中华人民共和国道路交通安全法》
(2012•宜宾一模)《中华人民共和国道路交通安全法》