题目内容
已知
得顶点
、
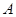分别是离心率为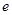
的圆锥曲线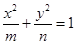
的焦点，顶点
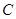在该曲线上，一同学已正确地推得，当
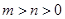时有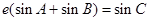
，类似地，当
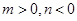时，有 .
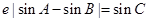
解析试题分析：猜想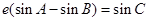
证明：当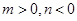时，圆锥曲线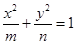为双曲线，设双曲线的焦距为
，实轴为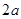
，
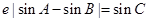∵，由正弦定理得，∴
，∴
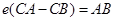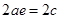恒成立.
考点：椭圆，双曲线的性质，正弦定理，合情推理.
练习册系列答案
相关题目
题目内容
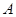已知得顶点、分别是离心率为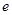的圆锥曲线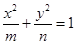的焦点，顶点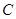在该曲线上，一同学已正确地推得，当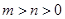时有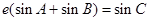 ，类似地，当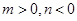时，有 .
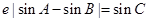
解析试题分析：猜想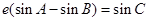
证明：当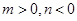时，圆锥曲线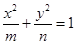为双曲线，设双曲线的焦距为，实轴为，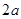
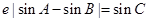∵，由正弦定理得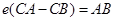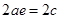，∴，∴恒成立.
考点：椭圆，双曲线的性质，正弦定理，合情推理.
的左顶点
作直线
交
轴于点
，交椭圆于点
，若
是等腰三角形，且
，则椭圆的离心率为 .
的离心率为2，则
的值为 ______．
、
是双曲线
的两个焦点，点
在此双曲线上，
，如果点
轴的距离等于
，那么该双曲线的离心率等于 ．
的离心率为
，顶点与椭圆
的焦点相同，那么双曲线的焦点坐标为_____；渐近线方程为_________.
是双曲线
的左焦点，
是双曲线右支上的动点，则
的最小值为 .
上一点
作圆
的切线
，若
对称，则点
的距离为 .
所经过的定点
恰好是椭圆
的一个焦点,且椭圆