题目内容
已知直线l:(a-2)y=(3a-1)x-1①求证:无论a为何值时,直线总过第一象限;②为使这条直线不过第二象限,求a的取值范围;③若直线l交x轴负半轴于A,交y轴正半轴于B.△AOB的面积为S且-2≤a≤-1,求S的最小值并求此时直线l的方程.
【答案】分析:①由于(3x-y)+(-x+2y-1)=0对任意实数a恒过直线3x-y=0与x-2y+1=0的交点即可得出结论;
②先对a进行分类讨论:当a=2时,直线为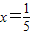 ,不过第二象限;当a≠2时,a≥2时直线不过第二象限.从而得到结果;
,不过第二象限;当a≠2时,a≥2时直线不过第二象限.从而得到结果;
③令x=0和令y=0得到直线在坐标轴上截距,再利用三角形面积公式得到S关于a的函数表达式,最后利用函数的单调性求得其最小值并求此时直线l的方程.
解答:解:①∵(3x-y)+(-x+2y-1)=0对任意实数a恒过直线3x-y=0与x-2y+1=0的交点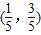 .
.
∴直线系恒过第一象限内的定点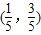 .
.
②当a=2时,直线为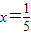 ,不过第二象限;当a≠2时,直线方程化为
,不过第二象限;当a≠2时,直线方程化为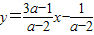
不过第二象限的充要条件为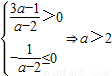
∴a≥2时直线不过第二象限.
③令x=0得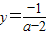
令y=0得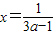 ∴
∴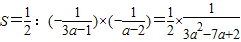
∵S在a∈[-2,-1]↗∴当a=-2时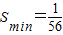
此时l:7x-4y+1=0
点评:本小题主要考查直线的方程、确定直线位置的几何要素、恒过定点的直线等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
②先对a进行分类讨论:当a=2时,直线为
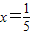 ,不过第二象限;当a≠2时,a≥2时直线不过第二象限.从而得到结果;
,不过第二象限;当a≠2时,a≥2时直线不过第二象限.从而得到结果;③令x=0和令y=0得到直线在坐标轴上截距,再利用三角形面积公式得到S关于a的函数表达式,最后利用函数的单调性求得其最小值并求此时直线l的方程.
解答:解:①∵(3x-y)+(-x+2y-1)=0对任意实数a恒过直线3x-y=0与x-2y+1=0的交点
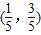 .
.∴直线系恒过第一象限内的定点
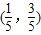 .
.②当a=2时,直线为
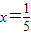 ,不过第二象限;当a≠2时,直线方程化为
,不过第二象限;当a≠2时,直线方程化为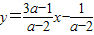
不过第二象限的充要条件为
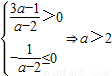
∴a≥2时直线不过第二象限.
③令x=0得
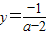
令y=0得
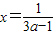 ∴
∴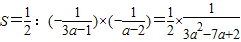
∵S在a∈[-2,-1]↗∴当a=-2时
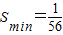
此时l:7x-4y+1=0
点评:本小题主要考查直线的方程、确定直线位置的几何要素、恒过定点的直线等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目