题目内容
已知直线l经过点A(2,4),且被平行直线l1:x-y+1=0与l2:x-y-1=0所截得的线段的中点M在直线x+y-3=0上.求直线l的方程.
[解析] 解法一:∵点M在直线x+y-3=0上,
∴设点M坐标为(t,3-t),则点M到l1、l2的距离相等,
即![]() =
=![]() ,
,
解得t=![]() ,∴M
,∴M![]() .
.
又l过点A(2,4),
由两点式得![]() =
=![]() ,
,
即5x-y-6=0,
故直线l的方程为5x-y-6=0.
解法二:设与l1、l2平行且距离相等的直线l3:x-y+c=0,由两平行直线间的距离公式得![]() =
=![]() ,解得c=0,即l3:x-y=0.由题意得中点M在l3上,又点M在x+y-3=0上.
,解得c=0,即l3:x-y=0.由题意得中点M在l3上,又点M在x+y-3=0上.
解方程组![]() ,得
,得![]() .
.
∴M![]() .又l过点A(2,4),
.又l过点A(2,4),
故由两点式得直线l的方程为5x-y-6=0.
解法三:由题意知直线l的斜率必存在,
设l:y-4=k(x-2),
由![]() ,得
,得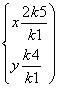 .
.
∴直线l与l1、l2的交点分别为![]() ,
,
![]() .
.
∵M为中点,∴M![]() .
.
又点M在直线x+y-3=0上,
∴![]() +
+![]() -3=0,解得k=5.
-3=0,解得k=5.
故所求直线l的方程为y-4=5(x-2),
即5x-y-6=0.

练习册系列答案
相关题目