题目内容
已知真命题:过椭圆
+
=1(a>b>0)左顶点A(-a,0)作两条互相垂直的直线,分别交椭圆于另外两点M、N,则直线MN过定点P(
,0).类比此命题,写出关于抛物线y2=2px(p>0)的一个真命题:
| x2 |
| a2 |
| y2 |
| b2 |
| a(a2-b2) |
| a2+b2 |
过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0)
过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0)
.分析:由类比推理,来得到关于抛物线的类似结论,易知在抛物线中有“过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0)”求解即可.
解答:解:已知过椭圆
+
=1(a>b>0)左顶点A(-a,0)作两条互相垂直的直线,分别交椭圆于另外两点M、N,则直线MN过定点P(
,0).
类比此命题,取特殊的抛物线:直线l与抛物线y2=2x相交于A、B两点,O为抛物线的顶点,若OA⊥OB.证明:直线l过定点如下:
证明:设点A,B的坐标分别为(x1,y1),(x2,y2)
(I)当直线l有存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.(2分)
联立方程得:
消去y得k2x2+(2kb-2)x+b2=0
由题意:x1x2=
y1y2=(kx1+b)(kx2+b)=
(5分)
又由OA⊥OB得x1x2+y1y2=0,(7分)
即
+
=0,解得b=0(舍去)或b=-2k(9分)
故直线l的方程为:y=kx-2k=k(x-2),故直线过定点(2,0)(11分)
(II)当直线l不存在斜率时,设它的方程为x=m,显然m>0
联立方程得:
解得 y=±
,即y1y2=-2m
又由OA⊥OB得x1x2+y1y2=0,即m2-2m=0,解得m=0(舍去)或m=2
可知直线l方程为:x=2,故直线过定点(2,0)
综合(1)(2)可知,满足条件的直线过定点(2,0).
故写出关于抛物线y2=2px(p>0)的一个真命题:过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0)
故答案为:过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0).
| x2 |
| a2 |
| y2 |
| b2 |
| a(a2-b2) |
| a2+b2 |
类比此命题,取特殊的抛物线:直线l与抛物线y2=2x相交于A、B两点,O为抛物线的顶点,若OA⊥OB.证明:直线l过定点如下:
证明:设点A,B的坐标分别为(x1,y1),(x2,y2)
(I)当直线l有存在斜率时,设直线方程为y=kx+b,显然k≠0且b≠0.(2分)
联立方程得:
|
由题意:x1x2=
| b2 |
| k2 |
|
| 2b |
| k |
又由OA⊥OB得x1x2+y1y2=0,(7分)
即
| b2 |
| k2 |
| 2b |
| k |
故直线l的方程为:y=kx-2k=k(x-2),故直线过定点(2,0)(11分)
(II)当直线l不存在斜率时,设它的方程为x=m,显然m>0
联立方程得:
|
| 2m |
又由OA⊥OB得x1x2+y1y2=0,即m2-2m=0,解得m=0(舍去)或m=2
可知直线l方程为:x=2,故直线过定点(2,0)
综合(1)(2)可知,满足条件的直线过定点(2,0).
故写出关于抛物线y2=2px(p>0)的一个真命题:过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0)
故答案为:过抛物线y2=2px(p>0)的顶点O作两条互相垂直的直线,分别交抛物线于另外两点M、N,则直线MN过定点P(2p,0).
点评:本题主要考查类比推理,可以先猜测在抛物线中成立的命题在椭圆里面也成立.再计算在这个具体的椭圆里面所求的定值.关于椭圆的一个恒等式:“
+
=
”是一个经常用到的式子,在以后的学习过程中希望大家多总结.
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2a |
| b2 |

练习册系列答案
相关题目

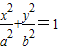 (a>b>0)上的一点,F1、F2是左、右两个焦点,若△PF1F2的内切圆的半径为
(a>b>0)上的一点,F1、F2是左、右两个焦点,若△PF1F2的内切圆的半径为 ,则此椭圆的离心率
,则此椭圆的离心率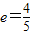 ;
;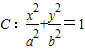 (a>b>0)上的任意一动点M,引圆O:x2+y2=b2的两条切线MA、MB,切点分别为A、B,若
(a>b>0)上的任意一动点M,引圆O:x2+y2=b2的两条切线MA、MB,切点分别为A、B,若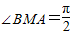 ,则椭圆的离心率e的取值范围为
,则椭圆的离心率e的取值范围为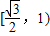 ;
; 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )