题目内容
已知p：“过定点（0，1）的动直线l恒与椭圆x2+| y2 |
| a |
| 1 |
| 3 |
分析：根据复合命题真假之间的关系，求出对应的a的取值范围即可得到结论．
解答：解：若p为真，则直线l过的定点（0，1）必在椭圆内部，即0＜
＜1⇒a＞1，
若q为真，则f'（x）=x2+2ax+2a=0有两个相异的实数根，
即得△＞0⇒4a2-8a＞0⇒a＞2或a＜0，
由p且q为假，p或q为真得：
或
，
∴实数a的取值范围a＜0或1＜a≤2．
| 1 |
| a |
若q为真，则f'（x）=x2+2ax+2a=0有两个相异的实数根，
即得△＞0⇒4a2-8a＞0⇒a＞2或a＜0，
由p且q为假，p或q为真得：
|
|
∴实数a的取值范围a＜0或1＜a≤2．
点评：本题主要复合命题之间的关系，先判断命题的真假关系是解决本题的关键．
练习册系列答案
相关题目
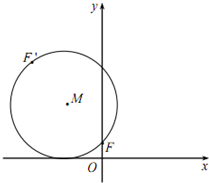（2012•深圳二模）如图，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C．
的最大值，并求取得这个最大值时α的值和此时圆C的方程.
的最大值，并求取得这个最大值时α的值和此时圆C的方程.
的最大值，并求取得这个最大值时α的值和此时圆C的方程。