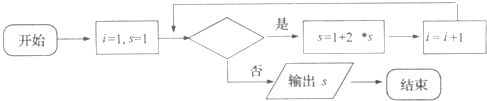
题目内容
【题目】函数f（x）=ax3+bx2+cx+d的图象如图，则函数y=ax2+ 
bx+ 
的单调递增区间是（ ） 
A.（﹣∞，2]
B.
，+∞）
C.[﹣2，3]
D.
，+∞）
【答案】D
【解析】解：不妨取a=1，
∵f（x）=x3+bx2+cx，∴f'（x）=3x2+2bx+c
由图可知f'（﹣2）=0，f'（3）=0
∴12﹣4b+c=0，27+6b+c=0，∴b=﹣1.5，c=﹣18
∴y=x2﹣ 
x﹣6，y'=2x﹣ ，当x＞ 
时，y'＞0
∴y=x2﹣x﹣6的单调递增区间为：[ ，+∞）
故选D．
【考点精析】关于本题考查的二次函数的性质和利用导数研究函数的单调性，需要了解当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减；一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能得出正确答案．
练习册系列答案
相关题目
