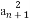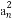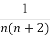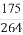Question

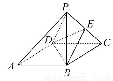
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)

 

 

Answer 1

见解析

【解析】【证明】(1)三角形的中位线与底边平行(大前提),

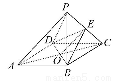
连接AC交BD于O,连接OE,由已知OE为△PAC的中位线(小前提),

所以PA∥OE(结论).

(2)平面外一条直线和平面内一直线平行,则平面外的直线与该平面平行(大前提),

PA?平面BDE,OE?平面BDE(小前提),

所以PA∥平面BDE(结论).

上面的证明可简略地写成:

连接AC交BD于O.连接OE,

∵四边形ABCD为平行四边形,

∴O为AC的中点.

又∵E为PC的中点,

∴在△PAC中,PA∥OE,OE?平面BDE,PA?平面BDE,

∴PA∥平面BDE.