题目内容
11.在锐角△ABC中,∠A=30°,O为△ABC所在平面内一点,满足$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$cosB+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$cosC=$\overrightarrow{AO}$,则|$\overrightarrow{AO}$|=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 不妨假设锐角△ABC为等腰三角形,可得∠B=∠C=75°,求得cosB=cosC=cos75°的值,再利用两个向量的数量积的运算公式求得,|$\overrightarrow{AO}$|=$\sqrt{{(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}cosB+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}cosC)}^{2}}$ 的值.
解答 解:不妨假设锐角△ABC为等腰三角形,则由∠A=30°,可得∠B=∠C=75°,
∴cosB=cosC=cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=$\frac{\sqrt{6}-\sqrt{2}}{4}$.
由题意可得,|$\overrightarrow{AO}$|=$\sqrt{{(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}cosB+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}cosC)}^{2}}$=$\sqrt{{cos}^{2}B{+cos}^{2}C+2cosBcosC•cos30°}$
=$\sqrt{\frac{2-\sqrt{3}}{4}+\frac{2-\sqrt{3}}{4}+\sqrt{3}•\frac{2-\sqrt{3}}{4}}$=$\sqrt{\frac{2-\sqrt{3}}{4}•(2+\sqrt{3})}$=$\frac{1}{2}$,
故选:D.
点评 本题主要考查两角和的余弦公式的应用,求向量的模,两个向量的数量积的运算,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{3\sqrt{3}}{8}$ | B. | $\frac{9\sqrt{3}}{16}$ | C. | $\frac{9\sqrt{3}}{8}$ | D. | $\frac{9\sqrt{3}}{4}$ |
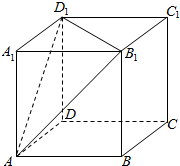 如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$. 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示: