题目内容
13．在y=2x2上有一点P，它到A（1，3）的距离与它到焦点的距离之和最小，求点P的坐标．分析 直线l为抛物线y=2x2的准线，F为其焦点，PN⊥l，AN1⊥l，由抛物线的定义知，|PF|=|PN|，可得|AP|+|PF|=|AP|+|PN|≥|AN1|，当且仅当A、P、N三点共线时取等号．
解答 
解：如图所示，直线l为抛物线y=2x2的准线，F为其焦点，PN⊥l，AN1⊥l，
由抛物线的定义知，|PF|=|PN|，
∴|AP|+|PF|=|AP|+|PN|≥|AN1|，当且仅当A、P、N三点共线时取等号．
∴P点的横坐标与A点的横坐标相同即为1，
∴P（1，2）．
点评 本题考查了抛物线的定义、标准方程及其性质、最小值问题，属于中档题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3．营养学家指出，成人良好的日常饮食应该至少提供75g的碳水化合物，60g的蛋白质，60g的脂肪，100g食物A含有12g的碳水化合物，8g的蛋白质，16g的脂肪，花费3元；而100g食物B含有12g的碳水化合物，16g的蛋白质，8g的脂肪，花费4元．
（Ⅰ）根据已知数据填写下表：
（Ⅱ）列车每天食用食物A和食物B所满足的不等式组；
（Ⅲ）为了满足营养学家指出的日常饮食要求，并且花费最低，每天需要食用食物A和食物B个多少g？
（Ⅰ）根据已知数据填写下表：
| 100g食物 | 碳水化合物/g | 蛋白质/g | 脂肪/g |
| A | |||
| B |
（Ⅲ）为了满足营养学家指出的日常饮食要求，并且花费最低，每天需要食用食物A和食物B个多少g？
8．（文）已知α∈R，sinα+2cosα=$\frac{\sqrt{10}}{2}$，则$\frac{（sinα+cosα+1）（sinα+cosα-1）}{（sinα-cosα）（sinα+cosα）}$=（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | -$\frac{4}{3}$ | D． | -$\frac{3}{4}$ |
5．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线被圆（x-a）2+y2=a2截得的弦长为$\sqrt{2}$a．则双曲线C的离心率为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
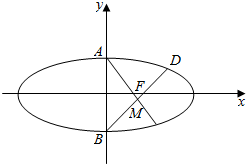已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，F为椭圆的右焦点，点A，B分别为椭圆的上下顶点，过点B作AF的垂线，垂足为M．