题目内容
2．已知 命题 M：2x-3＜7；命题N：x2-7x+10≤0．求：（1）命题￢N中x的范围？
（2）命题（￢M）∩N中x的范围？
分析 分别解出关于命题M，N中的x的范围，再求出￢M和￢N，结合集合的运算性质解出即可．
解答 解：（1）∵x2-7x+10≤0，解得：2≤x≤5，
∴N：[2，5]，
∴命题￢N中x的范围是：（-∞，2）∪（5，+∞）；
（2）命题 M：2x-3＜7，
∴M：x＜5，
∴￢M：x≥5，
∴（￢M）∩N=[5，+∞）∩[2，5]=[5]．
点评 本题考查了复合命题的判断，考查集合问题，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．给出下列结论：①命题“?x∈R，sinx≠1”的否定是“?x∈R，sinx=1”；②命题p：x≠2或y≠3，命题q：x+y≠5则p是q的必要不充分条件；③数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分必要条件；④“在三角形ABC中，若sinA＞sinB，则A＞B”的逆命题是真命题；⑤“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”．其中正确的是（ ）
| A． | ③④ | B． | ①②④⑤ | C． | ①③④⑤ | D． | ①②③④⑤ |
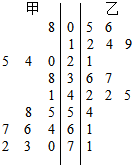为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00～10：00间