题目内容
过抛物线焦点F的直线交抛物线于A、B两点,通过点B平行于抛物线对称轴的直线交抛物线的准线于点D,求证:三点A、O、D共线.
分析:建系写方程,写出点A、B、D的坐标,可利用斜率相等,或用向量法证明三点共线.
解答:解:以抛物线的对称轴为x轴,它的顶点为原点,建立直角坐标系,
则可设抛物线的方程为y2=2px(p>0),
当直线AB的斜率存在时,设AB的斜率为k(k≠0),
由题意直线AB的方程为y=k(x-
),
把y=k(x-
)代入抛物线的方程得y2-
y-p2=0,
设点A(x1,y1),B(x2,y2),则y2=-
(y1≠0),D(-
,-
),
故可得kOA=
=
=
,而kOD=
=
=kOA,故三点A、O、D共线,
当直线无斜率时,A(
,p),B(
,-p),故D(-
,-p),
同样可得kOA=
=2,而kOD=
=2=kOA,仍有三点A、O、D共线,
综上可得三点A、O、D共线.
则可设抛物线的方程为y2=2px(p>0),
当直线AB的斜率存在时,设AB的斜率为k(k≠0),
由题意直线AB的方程为y=k(x-
| p |
| 2 |
把y=k(x-
| p |
| 2 |
| 2p |
| k |
设点A(x1,y1),B(x2,y2),则y2=-
| p2 |
| y1 |
| p |
| 2 |
| p2 |
| y1 |
故可得kOA=
| y1 |
| x1 |
| y1 | ||
|
| 2p |
| y1 |
-
| ||
-
|
| 2p |
| y1 |
当直线无斜率时,A(
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
同样可得kOA=
| p | ||
|
| -p | ||
-
|
综上可得三点A、O、D共线.
点评:本题考查三点共线的证明,涉及分类讨论的思想,属基础题.

练习册系列答案
相关题目
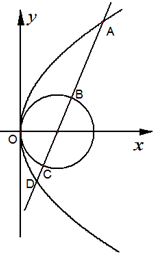 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).