题目内容
10.设函数$f(x)={x^3}-\frac{3(t+1)}{2}{x^2}+3tx+1$(t>0).(1)若t=2,求函数f(x)的极大值;
(2)若存在x0∈(0,2),使得f(x0)是f(x)在区间[0,2]上的最小值,求实数t的取值范围;
(3)若f(x)≤xex-m(e≈2.718)对任意的x∈[0,+∞)恒成立时m的最大值为-1,求实数t的取值范围.
分析 (1)由t=2,化简函数的解析式,求出函数的导数,利用导数为0,求出极值点,判断单调性如此极大值.(2)求出函数的导数,利用导数为0,求出极值点,通过①当t≥2时,②当1<t<2时,③当0<t<1时,④当t=1时,分别求解x0∈(0,2)使得f(x0)是f(x)在[0,2]上的最小值.推出t的取值范围.
(3)由题意转化条件为$m≤x{e^x}-{x^3}+\frac{3(t+1)}{2}{x^2}-3tx-1=x[{e^x}-{x^2}+\frac{3(t+1)}{2}x-3t]-1$对任意的x≥0恒成立,构造函数$g(x)={e^x}-{x^2}+\frac{3(t+1)}{2}x-3t$,通过函数的导数,求出新函数的最小值,然后求解t的取值范围.
解答 解:(1)若t=2,则$f(x)={x^3}-\frac{9}{2}{x^2}+6x+1$,
所以,f′(x)=3x2-9x+6,令f′(x)=0,得x=1,2;
令f′(x)<0,得1<x<2,
所以,f(x)在区间(1,2)内递减,在区间(-∞,1),(2,+∞)内递增,
得f(x)的极大值为$f(1)=\frac{7}{2}$…4'
(2)函数$f(x)={x^3}-\frac{3(t+1)}{2}{x^2}+3tx+1$.
得f′(x)=3x2-3(t+1)x+3t=3(x-1)(x-t),t>0.
令f′(x)=0,得x=1,t;…6'
①当t≥2时,可以判定f(x)在区间(0,1)内递增,在区间(1,2)内递减,
此时,不存在x0∈(0,2)使得f(x0)是f(x)在[0,2]上的最小值;
②当1<t<2时,可以判定f(x)在区间(0,1)、(t,2)内递增,在区间(1,t)内递减,
欲存在x0∈(0,2)使得f(x0)是f(x)在[0,2]上的最小值,
则必须有f(t)≤f(0),即${t^3}-\frac{3(t+1)}{2}{t^2}+3{t^2}+1≤1$,解得t≥3,不合题意,舍去.
③当0<t<1时,可以判定f(x)在区间(0,t)、(1,2)内递增,在区间(t,1)内递减,
欲存在x0∈(0,2)使得f(x0)是f(x)在[0,2]上的最小值,
则必须有f(1)≤f(0),即$\frac{3t+1}{2}≤1$,解得$t≤\frac{1}{3}$,所以,$0<t≤\frac{1}{3}$.
④当t=1时,可以判定f(x)在区间(0,2)内递增,
不存在x0∈(0,2)使得f(x0)是f(x)在[0,2]上的最小值.
综上所述,得t的取值范围为$(0,\frac{1}{3}]$…10'
(3)若f(x)≤xex-m(e为自然对数的底数)对任意的x∈[0,+∞)恒成立,
即 $m≤x{e^x}-{x^3}+\frac{3(t+1)}{2}{x^2}-3tx-1=x[{e^x}-{x^2}+\frac{3(t+1)}{2}x-3t]-1$对任意的x≥0恒成立,…11'
令$g(x)={e^x}-{x^2}+\frac{3(t+1)}{2}x-3t$,由于m的最大值为-1,
所以$g(x)={e^x}-{x^2}+\frac{3(t+1)}{2}x-3t≥0$恒成立…12'
由g(0)=1-3t≥0可得$0<t≤\frac{1}{3}$,
当$0<t≤\frac{1}{3}$时,$g'(x)={e^x}-2x+\frac{3(t+1)}{2}$,
再设$h(x)=g'(x)={e^x}-2x+\frac{3(t+1)}{2}$,得h′(x)=ex-2=0,解得x=ln2.h(x)在区间(0,ln2)内递减,在区间(ln2,+∞)内递增,h(x)的最小值为$h(ln2)=2+\frac{3(t+1)}{2}-2ln2$,可以判定h(ln2)>0,
即g′(x)>0,所以g(x)在区间[0,+∞)内递增,
则有g(x)在区间[0,+∞)内的最小值g(0)=1-3t≥0,得$t≤\frac{1}{3}$.
所以,t的取值范围是$(0,\frac{1}{3}]$…16'
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性,函数的最值的求法,考查转化思想,分类讨论思想的应用,考查计算能力.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
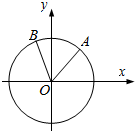 如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求
如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求