题目内容
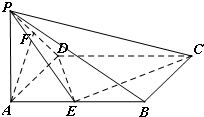 (2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.
(2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.(Ⅰ)当E是AB的中点时,求证:AF∥平面PEC;
(Ⅱ)要使二面角P-EC-D的大小为45°,试确定E点的位置.
分析:法一:
(I)取PC的中点O,连接OF,OE.由已知得OF∥DC且OF=
DC,由E是AB的中点,则OF∥AE且OF=AE,故AEOF是平行四边形,由此能够证明AF∥平面PEC.
(II)作AM⊥CE交CE的延长线于M.连接PM,由三垂线定理得PM⊥CE,∠PMA是二面角P-EC-D的平面角.由此能够推导出要使二面角P-EC-D的大小为45°,只需AE=
.
解法二:
(I)由已知,AB,AD,AP两两垂直,分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.利用向量法能够证明AF∥平面PEC.
(II)求出平面DEC的一个法向量为
=(0,0,1),设E=(t,0,0),求出平面PEC的法向量为
=(1,t-2,t),利用向量法能求出要使要使二面角P-EC-D的大小为45°,只需AE=
.
(I)取PC的中点O,连接OF,OE.由已知得OF∥DC且OF=
| 1 |
| 2 |
(II)作AM⊥CE交CE的延长线于M.连接PM,由三垂线定理得PM⊥CE,∠PMA是二面角P-EC-D的平面角.由此能够推导出要使二面角P-EC-D的大小为45°,只需AE=
| 5 |
| 4 |
解法二:
(I)由已知,AB,AD,AP两两垂直,分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.利用向量法能够证明AF∥平面PEC.
(II)求出平面DEC的一个法向量为
| AP |
| m |
| 5 |
| 4 |
解答: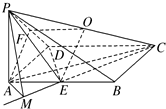 解法一:
解法一:
(I)证明:如图,取PC的中点O,连接OF,OE.
由已知得OF∥DC且OF=
DC,
又∵E是AB的中点,则OF∥AE且OF=AE,
∴AEOF是平行四边形,
∴AF∥OE
又∵OE?平面PEC,AF?平面PEC
∴AF∥平面PEC.
(II)解:如图,作AM⊥CE交CE的延长线于M.
连接PM,由三垂线定理得PM⊥CE,
∴∠PMA是二面角P-EC-D的平面角.
∴∠PMA=45°,
∵PA=1,∴AM=1,
设AE=x,
由△AME≌△CBE,得x=
,解得x=
,
故要使二面角P-EC-D的大小为45°,只需AE=
.
解法二:
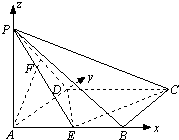
(I)证明:由已知,AB,AD,AP两两垂直,
分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),F(0,
,
),
∴
=(0,
,
),
∵E(1,0,0),C(2,1,0),P(0,0,1),
设平面PEC的法向量为
=(x,y,z)
则
⇒
, 令x=1得
令x=1得
=(1,-1,1),
由
•
=(0,
,
)•(1,-1,1)=0,得
⊥
,
又AF?平面PEC,故AF∥平面PEC.
(II)解:由已知可得平面DEC的一个法向量为
=(0,0,1),
设E=(t,0,0),设平面PEC的法向量为
=(x,y,z)
则
⇒
,令x=1得
=(1,t-2,t),
由cos45o=|
|⇒t=
,
故,要使要使二面角P-EC-D的大小为45°,只需AE=
.
 解法一:
解法一:(I)证明:如图,取PC的中点O,连接OF,OE.
由已知得OF∥DC且OF=
| 1 |
| 2 |
又∵E是AB的中点,则OF∥AE且OF=AE,
∴AEOF是平行四边形,
∴AF∥OE
又∵OE?平面PEC,AF?平面PEC
∴AF∥平面PEC.
(II)解:如图,作AM⊥CE交CE的延长线于M.
连接PM,由三垂线定理得PM⊥CE,
∴∠PMA是二面角P-EC-D的平面角.
∴∠PMA=45°,
∵PA=1,∴AM=1,
设AE=x,
由△AME≌△CBE,得x=
| (2-x)2+1 |
| 5 |
| 4 |
故要使二面角P-EC-D的大小为45°,只需AE=
| 5 |
| 4 |
解法二:
(I)证明:由已知,AB,AD,AP两两垂直,
分别以它们所在直线为x,y,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),F(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
∵E(1,0,0),C(2,1,0),P(0,0,1),
设平面PEC的法向量为
| m |
则
|
|
 令x=1得
令x=1得| m |
由
| AF |
| m |
| 1 |
| 2 |
| 1 |
| 2 |
| AF |
| m |
又AF?平面PEC,故AF∥平面PEC.
(II)解:由已知可得平面DEC的一个法向量为
| AP |
设E=(t,0,0),设平面PEC的法向量为
| m |
则
|
|
| m |
由cos45o=|
| ||||
|
|
| 5 |
| 4 |
故,要使要使二面角P-EC-D的大小为45°,只需AE=
| 5 |
| 4 |
点评:本题考查直线与平面平行的证明,考查要使二面角的大小为45°的点的位置的确定.解题时要认真审题,合理地化空间问题为平面问题,注意向量法的合理运用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目