题目内容
设存在复数z同时满足下列条件:(1)复数z在复平面内对应的点位于第二象限;
(2)z·z+2iz=8+ai(a∈R),试求a的取值范围.
分析:由(2)知复数相等,需表示出两边复数的实部、虚部.需设出复数z,再根据复数相等的充要条件转化.
解:设z=m+ni(m、n∈R),
∴z![]() =m2+n2.
=m2+n2.
由(1)知m<0,n>0.
则(2)化为m2+n2+2i(m+ni)=8+ai,
即m2+n2-2n+2mi=8+ai.
∴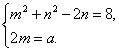
∴a2=4m2=4(8-n2+2n)=4[-(n-1)2+9].
∵n>0,∴a2≤36.
∴|a|≤6.
又∵m<0,∴a<0.
∴-6≤a<0.
绿色通道
本题主要利用复数相等的充要条件转化成方程组求解,再利用(1)的限制条件求a的范围.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 +2iz=8+ai (a∈R),试求a的取值范围.
+2iz=8+ai (a∈R),试求a的取值范围.