题目内容
:已知函数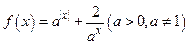 ,
,
(1)若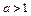 ,且关于
,且关于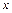 的方程
的方程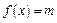 有两个不同的正数解,求实数
有两个不同的正数解,求实数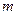 的取值范围;
的取值范围;
(2)设函数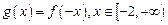 ,
,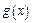 满足如下性质:若存在最大(小)值,则最大(小)值与
满足如下性质:若存在最大(小)值,则最大(小)值与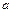 无关.试求
无关.试求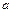 的取值范围.
的取值范围.
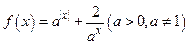 ,
,(1)若
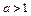 ,且关于
,且关于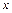 的方程
的方程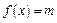 有两个不同的正数解,求实数
有两个不同的正数解,求实数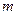 的取值范围;
的取值范围;(2)设函数
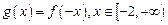 ,
,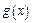 满足如下性质:若存在最大(小)值,则最大(小)值与
满足如下性质:若存在最大(小)值,则最大(小)值与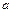 无关.试求
无关.试求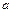 的取值范围.
的取值范围.:略
:解:(1)令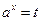 ,
,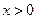 ,因为
,因为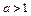 ,所以
,所以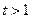 ,所以关于
,所以关于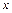 的方程
的方程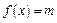 有两个不同的正数解等价于关于
有两个不同的正数解等价于关于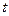 的方程
的方程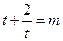 有相异的且均大于1的两根,即关于
有相异的且均大于1的两根,即关于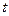 的方程
的方程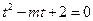 有相异的且均大于1的两根,……………………………………………………2分
有相异的且均大于1的两根,……………………………………………………2分
所以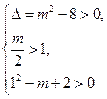 ,…………………………………………………………………4分
,…………………………………………………………………4分
解得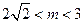 ,故实数
,故实数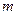 的取值范围为区间
的取值范围为区间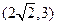 .……………………………6分
.……………………………6分
(2)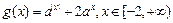
①当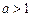 时,
时,
a)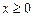 时,
时,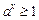 ,
,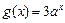 ,所以
,所以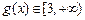 ,
,
b)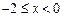 时,
时,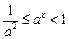
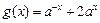 ,所以
,所以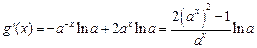 ……8分
……8分
ⅰ当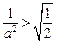 即
即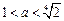 时,对
时,对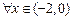 ,
,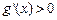 ,所以
,所以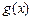 在
在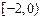 上递增,
上递增,
所以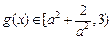 ,综合a) b)
,综合a) b)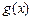 有最小值为
有最小值为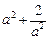 与a有关,不符合……10分
与a有关,不符合……10分
ⅱ当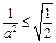 即
即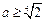 时,由
时,由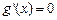 得
得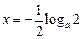 ,且当
,且当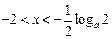 时,
时,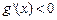 ,当
,当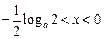 时,
时,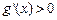 ,所以
,所以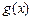 在
在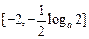 上递减,在
上递减,在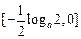 上递增,所以
上递增,所以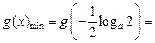
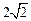 ,综合a) b)
,综合a) b) 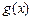 有最小值为
有最小值为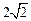 与a无关,符合要求.………12分
与a无关,符合要求.………12分
②当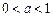 时,
时,
a)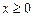 时,
时,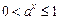 ,
,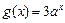 ,所以
,所以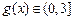
b)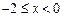 时,
时,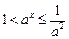 ,
,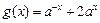 ,
,
所以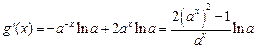
 ,
,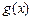 在
在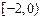 上递减,
上递减,
所以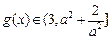 ,综合a) b)
,综合a) b) 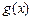 有最大值为
有最大值为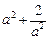 与a有关,不符合………14分
与a有关,不符合………14分
综上所述,实数a的取值范围是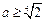 .………………………………………………16分
.………………………………………………16分
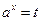 ,
,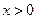 ,因为
,因为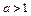 ,所以
,所以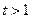 ,所以关于
,所以关于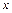 的方程
的方程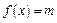 有两个不同的正数解等价于关于
有两个不同的正数解等价于关于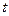 的方程
的方程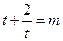 有相异的且均大于1的两根,即关于
有相异的且均大于1的两根,即关于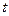 的方程
的方程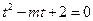 有相异的且均大于1的两根,……………………………………………………2分
有相异的且均大于1的两根,……………………………………………………2分所以
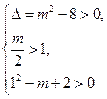 ,…………………………………………………………………4分
,…………………………………………………………………4分解得
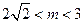 ,故实数
,故实数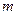 的取值范围为区间
的取值范围为区间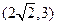 .……………………………6分
.……………………………6分(2)
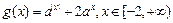
①当
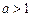 时,
时,a)
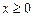 时,
时,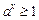 ,
,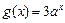 ,所以
,所以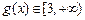 ,
,b)
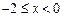 时,
时,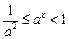
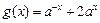 ,所以
,所以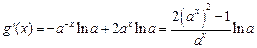 ……8分
……8分ⅰ当
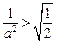 即
即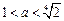 时,对
时,对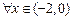 ,
,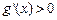 ,所以
,所以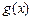 在
在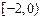 上递增,
上递增,所以
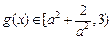 ,综合a) b)
,综合a) b)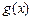 有最小值为
有最小值为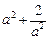 与a有关,不符合……10分
与a有关,不符合……10分ⅱ当
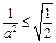 即
即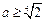 时,由
时,由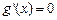 得
得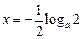 ,且当
,且当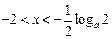 时,
时,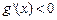 ,当
,当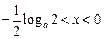 时,
时,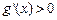 ,所以
,所以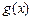 在
在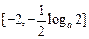 上递减,在
上递减,在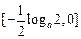 上递增,所以
上递增,所以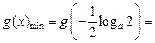
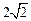 ,综合a) b)
,综合a) b) 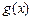 有最小值为
有最小值为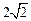 与a无关,符合要求.………12分
与a无关,符合要求.………12分②当
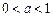 时,
时,a)
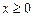 时,
时,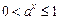 ,
,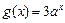 ,所以
,所以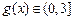
b)
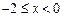 时,
时,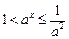 ,
,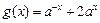 ,
,所以
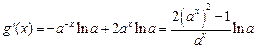
 ,
,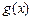 在
在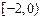 上递减,
上递减,所以
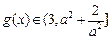 ,综合a) b)
,综合a) b) 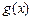 有最大值为
有最大值为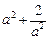 与a有关,不符合………14分
与a有关,不符合………14分综上所述,实数a的取值范围是
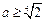 .………………………………………………16分
.………………………………………………16分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
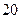 元购进一批商品,若该商品零售价定为
元购进一批商品,若该商品零售价定为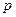 元,则销售量
元,则销售量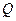 (单位:件)与零售价
(单位:件)与零售价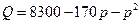 ,问该商品零售价定为多少时利润
,问该商品零售价定为多少时利润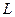 最大,并求出最大利润(利润
最大,并求出最大利润(利润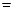 销售收入
销售收入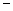 进货支出)
进货支出) ,若对
,若对
 ,
,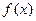 恒有两个零点,则函数
恒有两个零点,则函数 可为 ( )
可为 ( )



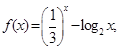 实数
实数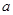 、
、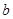 、
、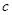 满足
满足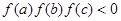 ,(0<
,(0<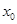 是函数
是函数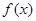 的一个零点,那么下列不等式中,不可能成立的是 ( )
的一个零点,那么下列不等式中,不可能成立的是 ( )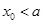
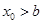
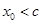
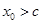
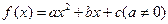 的图像过点
的图像过点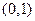 ,且有唯一的零点
,且有唯一的零点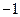 .
.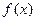 的表达式;
的表达式;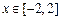 时,求函数
时,求函数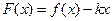 的最小值
的最小值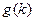 .
.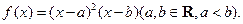
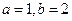 时,求曲线
时,求曲线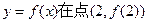 处的切线方程;
处的切线方程;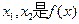 的两个极值点,
的两个极值点,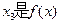 的一个零点,且
的一个零点,且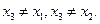 证明:存在实数
证明:存在实数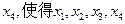 按照某种顺序排列后构成等差数列,并求
按照某种顺序排列后构成等差数列,并求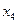 .
.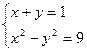 的解集是_____________.
的解集是_____________.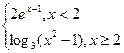 则不等式f(x)>2的解集为________________
则不等式f(x)>2的解集为________________ _
_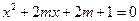
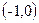 内,另一根在区间
内,另一根在区间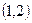 内,求m的取值范围
内,求m的取值范围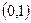 内,求m的取值范围
内,求m的取值范围