题目内容
(本小题满分13分)
已知函数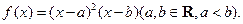
(1)当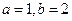 时,求曲线
时,求曲线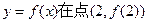 处的切线方程;
处的切线方程;
(2)设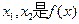 的两个极值点,
的两个极值点,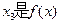 的一个零点,且
的一个零点,且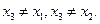 证明:存在实数
证明:存在实数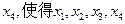 按照某种顺序排列后构成等差数列,并求
按照某种顺序排列后构成等差数列,并求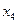 .
.
已知函数
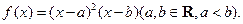
(1)当
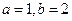 时,求曲线
时,求曲线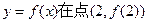 处的切线方程;
处的切线方程;(2)设
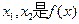 的两个极值点,
的两个极值点,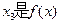 的一个零点,且
的一个零点,且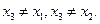 证明:存在实数
证明:存在实数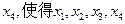 按照某种顺序排列后构成等差数列,并求
按照某种顺序排列后构成等差数列,并求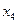 .
.(1)y="x" - 2
(2)
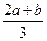
(本小题满分13分)
(1)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5) …………..2分
故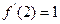 …………….3分
…………….3分
f(2)="0, " …………….4分
…………….4分
所以f(x)在点(2,0)处的切线方程为y="x" - 2 ………..5分
(2)证明:因为f′(x)=3(x-a)(x-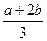 ),…………….7分
),…………….7分
由于a<b. 故a<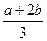 .
.
所以f(x)的两个极值点为x=a,x=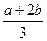 ………..9分
………..9分
不妨设x1=a,x2=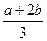 ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b. …………….10分
又因为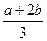 -a=2(b-
-a=2(b-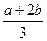 ),
),
x4=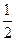 (a+
(a+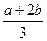 )=
)=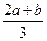 ,
,
所以a,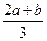 ,
,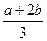 ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=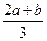 .…………………….13分
.…………………….13分
(1)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5) …………..2分
故
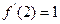 …………….3分
…………….3分f(2)="0, "
 …………….4分
…………….4分所以f(x)在点(2,0)处的切线方程为y="x" - 2 ………..5分
(2)证明:因为f′(x)=3(x-a)(x-
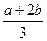 ),…………….7分
),…………….7分由于a<b. 故a<
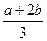 .
.所以f(x)的两个极值点为x=a,x=
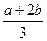 ………..9分
………..9分不妨设x1=a,x2=
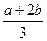 ,
,因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b. …………….10分
又因为
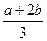 -a=2(b-
-a=2(b-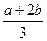 ),
),x4=
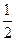 (a+
(a+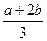 )=
)=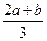 ,
,所以a,
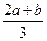 ,
,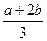 ,b依次成等差数列,
,b依次成等差数列, 所以存在实数x4满足题意,且x4=
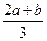 .…………………….13分
.…………………….13分
练习册系列答案
相关题目
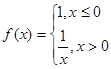 ,则使方程
,则使方程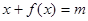 有解的实数
有解的实数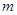 的取值范围
的取值范围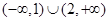
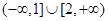
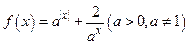 ,
,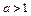 ,且关于
,且关于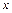 的方程
的方程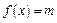 有两个不同的正数解,求实数
有两个不同的正数解,求实数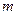 的取值范围;
的取值范围;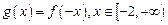 ,
,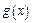 满足如下性质:若存在最大(小)值,则最大(小)值与
满足如下性质:若存在最大(小)值,则最大(小)值与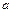 无关.试求
无关.试求 000元的电视机共3600台,每批都购入x台
000元的电视机共3600台,每批都购入x台 ,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰
,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰 当安排每批进货的数量,使资金够用?写出你的结论并说明理由
当安排每批进货的数量,使资金够用?写出你的结论并说明理由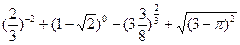 ;
;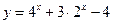 的零点.
的零点. ,如果
,如果 ,则
,则 ( )
( )



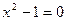 的解集用列举法表示为( )
的解集用列举法表示为( )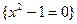
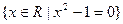
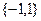
 )=
)=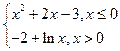 的零点个数为
的零点个数为